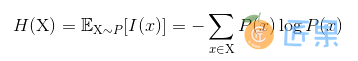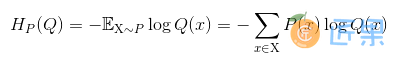逻辑斯蒂回归,决策树,支持向量机,梯度提升决策树 GBDT,随机森林
《深度学习》 3.13 信息论
- 非常可能发生的事件信息量要比较少,并且极端情况下,一定能够发生的事件应该没有信息量。
- 比较不可能发生的事件具有更大的信息量。
- 独立事件应具有增量的信息。例如,投掷的硬币两次正面朝上传递的信息量,应该是投掷一次硬币正面朝上的信息量的两倍。
信息熵 与 自信息
- 自信息 (self-information)是一种量化以上性质的函数,定义一个事件
x的自信息为:当该对数的底数为自然对数 e 时,单位为奈特(nats);当以 2 为底数时,单位为比特(bit)或香农(shannons)
- 自信息只处理单个的输出。
- 信息熵 (Information-entropy)用于对整个概率分布中的不确定性总量 进行量化:
信息论中,记
0log0 = 0
交叉熵 与 相对熵/KL散度
定义 P 对 Q 的 KL 散度 (Kullback-Leibler divergence):
KL 散度在信息论中度量的是哪个直观量?
- 在离散型变量的情况下, KL 散度衡量的是:当我们使用一种被设计成能够使得概率分布 Q 产生的消息的长度最小的编码,发送包含由概率分布 P 产生的符号的消息时,所需要的额外信息量。
KL散度的性质 :
- 非负;KL 散度为 0 当且仅当P 和 Q 在离散型变量的情况下是相同的分布,或者在连续型变量的情况下是“几乎处处”相同的
- 不对称;D_p(q) != D_q(p)
交叉熵 (cross-entropy):
信息量,信息熵,交叉熵,KL散度和互信息(信息增益) - CSDN博客
交叉熵 与 KL 散度的关系
- 针对 Q 最小化交叉熵等价于最小化 P 对 Q 的 KL 散度 ,因为 Q 并不参与被省略的那一项。
- 最大似然估计中,最小化 KL 散度其实就是在最小化分布之间的交叉熵。
下一节:逻辑斯蒂回归,决策树,支持向量机,梯度提升决策树 GBDT,随机森林