leveldb中内存数据库用来维护有序的key-value对,其底层是利用跳表实现,绝大多数操作(读/写)的时间复杂度均为O(logn),有着与平衡树相媲美的操作效率,但是从实现的角度来说简单许多,因此在本文中将介绍一下内存数据库的实现细节。
跳表
概述
跳表(SkipList)是由William Pugh提出的。他在论文《Skip lists: aprobabilistic alternative to balancedtrees》中详细地介绍了有关跳表结构、插入删除操作的细节。
这种数据结构是利用概率均衡 技术,加快简化插入、删除操作,且保证绝大大多操作均拥有O(logn)的良好效率。
作者在他的论文中这样介绍跳表:
平衡树(以红黑树为代表)是一种非常复杂的数据结构,为了维持树结构的平衡,获取稳定的查询效率,平衡树每次插入可能会涉及到较为复杂的节点旋转等操作。作者设计跳表的目的就是借助概率平衡 ,来构建一个快速且简单的数据结构,取代平衡树。
作者从链表讲起,一步步引出了跳表这种结构的由来。
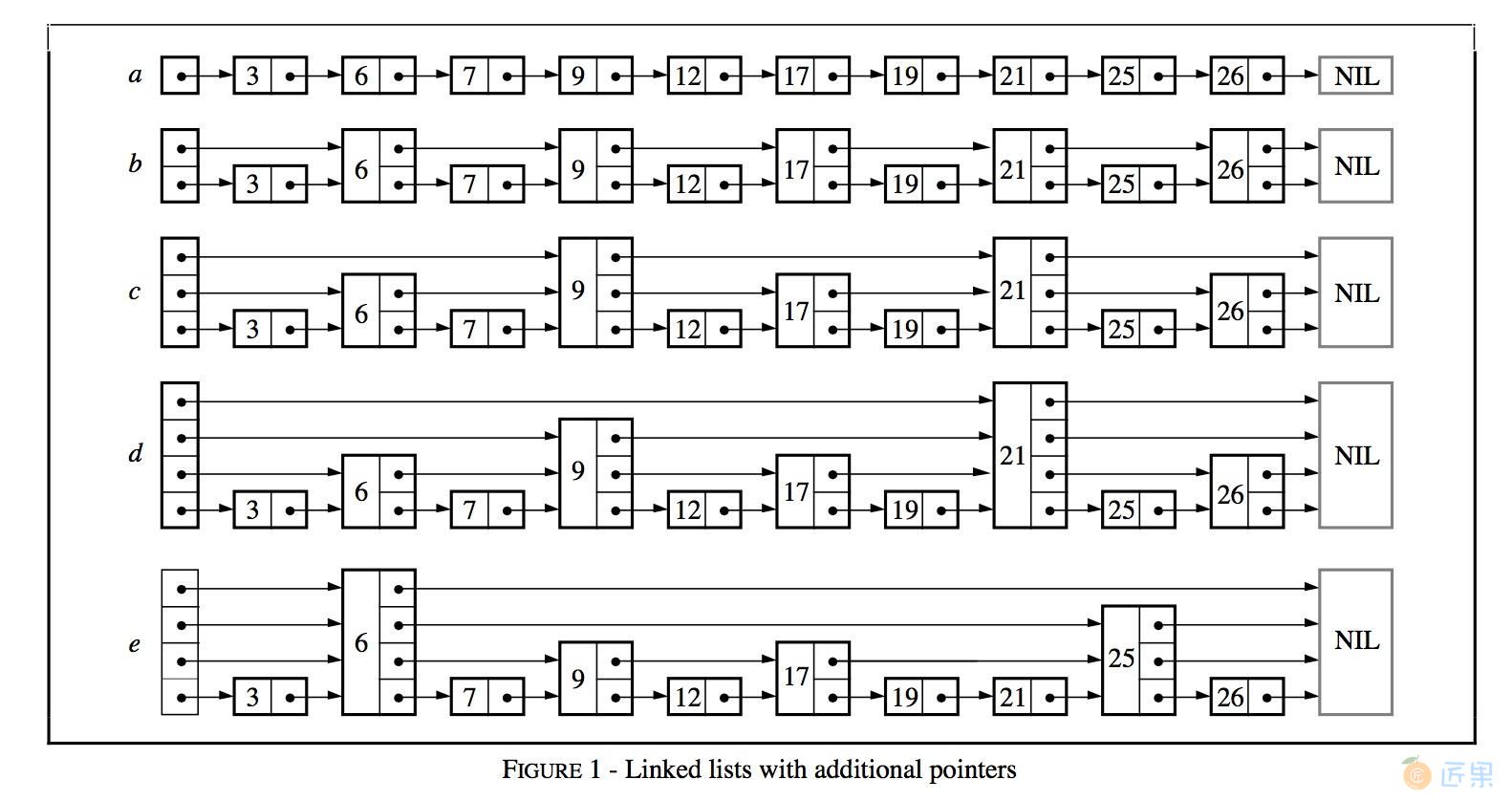
- 图a中,所有元素按序排列,被存储在一个链表中,则一次查询之多需要比较N个链表节点;
- 图b中,每隔2个链表节点,新增一个额外的指针,该指针指向间距为2的下一个节点,如此以来,借助这些额外的指针,一次查询至多只需要⌈n/2⌉+ 1次比较;
- 图c中,在图b的基础上,每隔4个链表节点,新增一个额外的指针,指向间距为4的下一个节点,一次查询至多需要⌈n/4⌉+ 2次比较;
作者推论,若每隔2^i个节点,新增一个辅助指针,最终一次节点的查询效率为O(logn)。但是这样不断地新增指针,使得一次插入、删除操作将会变得非常复杂。
一个拥有k 个指针的结点称为一个k 层结点(level knode )。按照上面的逻辑,50%的结点为1层节点,25%的结点为2层节点,12.5%的结点为3层节点。若保证每层节点的分布如上述概率所示,则仍然能够相同的查询效率。图e便是一个示例。
维护这些辅助指针将会带来较大的复杂度,因此作者将每一层中,每个节点的辅助指针指向该层中下一个节点。故在插入删除操作时,只需跟操作链表一样,修改相关的前后两个节点的内容即可完成,作者将这种数据结构称为跳表。
结构
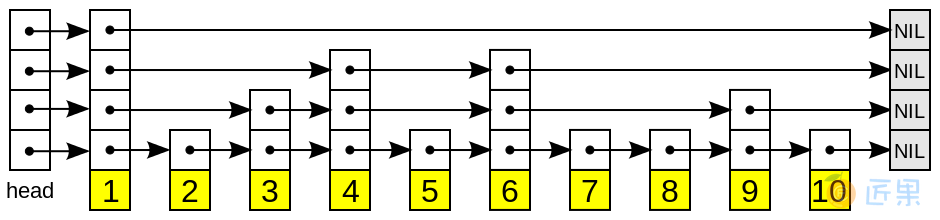
一个跳表的结构示意图如上所示。
跳跃列表是按层建造的。底层是一个普通的有序 链表。每个更高层都充当下面链表的"快速通道",这里在层i 中的元素按某个固定的概率 p (通常为0.5或0.25)出现在层 i +1中。平均起来,每个元素都在 1/(1-p )个列表中出现,而最高层的元素(通常是在跳跃列表前端的一个特殊的头元素)在O(log1/p__n ) 个列表中出现。
查找
在介绍插入和删除操作之前,我们首先介绍查找操作,该操作是上述两个操作的基础。
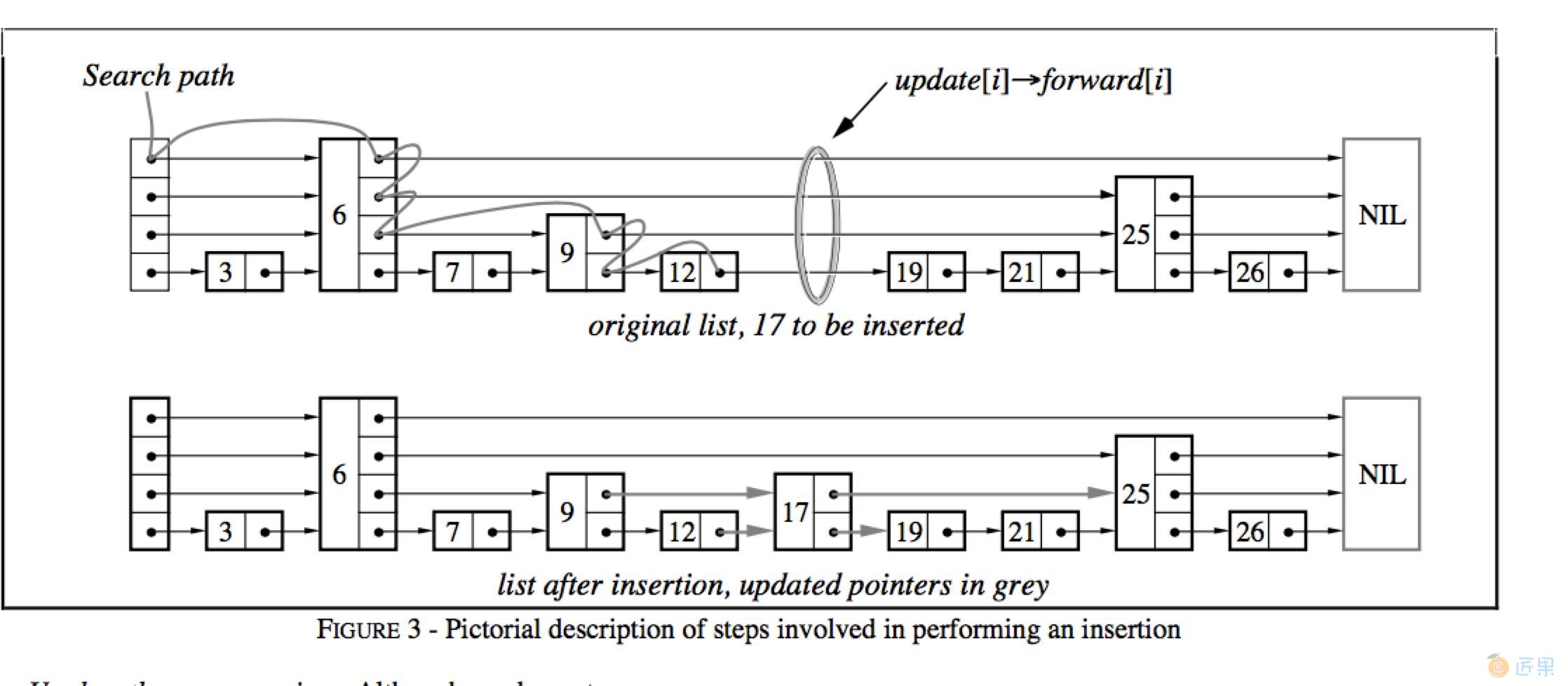
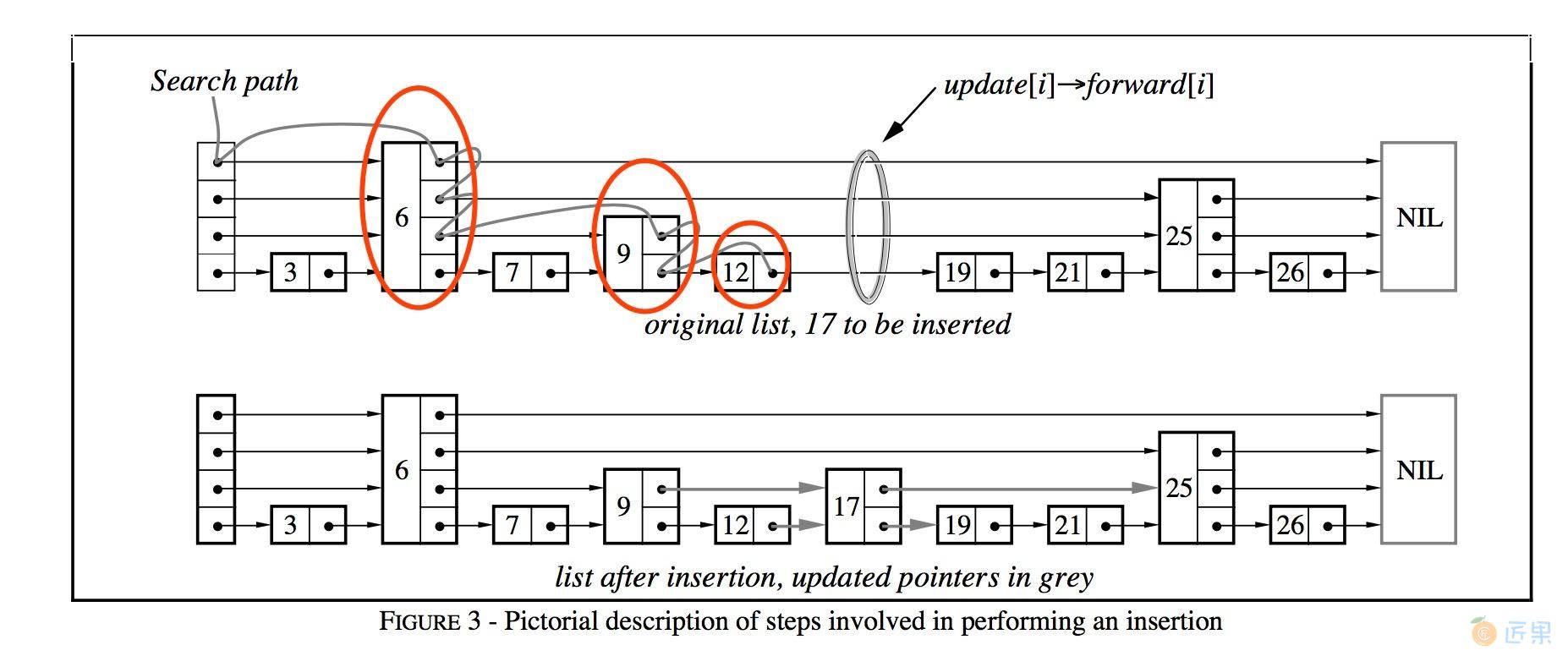
例如图中,需要查找一个值为17的链表节点,查找的过程为:
- 首先根据跳表的高度选取最高层的头节点;
- 若跳表中的节点内容小于查找节点的内容,则取该层的下一个节点继续比较;
- 若跳表中的节点内容等于查找节点的内容,则直接返回;
- 若跳表中的节点内容大于查找节点的内容,且层高不为0,则降低层高,且从前一个节点开始,重新查找低一层中的节点信息;若层高为0,则返回当前节点,该节点的key大于所查找节点的key。
综合来说,就是利用稀疏的高层节点,快速定位到所需要查找节点的大致位置,再利用密集的底层节点,具体比较节点的内容。
插入
插入操作借助于查找操作实现。
- 在查找的过程中,不断记录每一层 的前任节点 ,如图中红色圆圈所表示的;
- 为新插入的节点随机产生层高(随机产生层高的算法较为简单,依赖最高层数和概率值p,可见下文中的代码实现);
- 在合适的位置插入新节点(例如图中节点12与节点19之间),并依据查找时记录的前任节点信息,在每一层中,以链表插入 的方式,将该节点插入到每一层的链接中。
链表插入 指:将当前节点的Next值置为前任节点的Next值,将前任节点的Next值替换为当前节点。
func (p *DB) randHeight() (h int) {
const branching = 4
h = 1
for h < tMaxHeight && p.rnd.Int()%branching == 0 {
h++
}
return
}
删除
跳表的删除操作较为简单,依赖查找过程找到该节点在整个跳表中的位置后,以链表删除 的方式,在每一层中,删除该节点的信息。
链表删除 指:将前任节点的Next值替换为当前节点的Next值,并将当前节点所占的资源释放。
迭代
向后遍历
- 若迭代器刚被创建,则根据用户指定的查找范围[Start,Limit)找到一个符合条件的跳表节点;
- 若迭代器处于中部,则取出上一次访问的跳表节点的后继节点,作为本次访问的跳表节点(后继节点为最底层的后继节点);
- 利用跳表节点信息(keyvalue数据偏移量,key,value值长度等),获取keyvalue数据;
向前遍历
- 若迭代器刚被创建,则根据用户指定的查找范围[Start,Limit)在跳表中找到最后一个符合条件的跳表节点;
- 若迭代器处于中部,则利用上一次访问的节点的key值,查找比该key值更小的跳表节点;
- 利用跳表节点信息(keyvalue数据偏移量,key,value值长度等),获取keyvalue数据;
内存数据库
在介绍完跳表这种数据结构的组织原理以后,我们介绍leveldb如何利用跳表来构建一个高效的内存数据库。
键值编码
在介绍内存数据库之前,首先介绍一下内存数据库的键值编码规则。由于内存数据库本质是一个kv集合,且所有的数据项都是依据key值排序的,因此键值的编码规则尤为关键。
内存数据库中,key称为internalKey,其由三部分组成:
- 用户定义的key:这个key值也就是原生的key值;
- 序列号:leveldb中,每一次写操作都有一个sequencenumber,标志着写入操作的先后顺序。由于在leveldb中,可能会有多条相同key的数据项同时存储在数据库中,因此需要有一个序列号来标识这些数据项的新旧情况。序列号最大的数据项为最新值;
- 类型:标志本条数据项的类型,为更新还是删除;
键值比较
内存数据库中所有的数据项都是按照键值比较规则进行排序的。这个比较规则可以由用户自己定制,也可以使用系统默认的。在这里介绍一下系统默认的比较规则。
默认的比较规则:
- 首先按照字典序比较用户定义的key(ukey),若用户定义key值大,整个internalKey就大;
- 若用户定义的key相同,则序列号大的internalKey值就小;
通过这样的比较规则,则所有的数据项首先按照用户key进行升序排列;当用户key一致时,按照序列号进行降序排列,这样可以保证首先读到序列号大的数据项。
数据组织
以goleveldb为示例,内存数据库的定义如下:
type DB struct {
cmp comparer.BasicComparer
rnd *rand.Rand
mu sync.RWMutex
kvData []byte
// Node data:
// [0] : KV offset
// [1] : Key length
// [2] : Value length
// [3] : Height
// [3..height] : Next nodes
nodeData []int
prevNode [tMaxHeight]int
maxHeight int
n int
kvSize int
}
其中kvData用来存储每一条数据项的key-value数据,nodeData用来存储每个跳表节点的链接信息 。
nodeData中,每个跳表节点占用一段连续的存储空间,每一个字节分别用来存储特定的跳表节点信息。
- 第一个字节用来存储本节点key-value数据在kvData中对应的偏移量;
- 第二个字节用来存储本节点key值长度;
- 第三个字节用来存储本节点value值长度;
- 第四个字节用来存储本节点的层高;
- 第五个字节开始,用来存储每一层对应的下一个节点的索引值;
基本操作
Put 、Get 、Delete 、Iterator 等操作均依赖于底层的跳表的基本操作实现,不再赘述。
下一节:如我们之前提到的,leveldb是典型的LSM树(Log Structured-MergeTree)实现,即一次leveldb的写入过程并不是直接将数据持久化到磁盘文件中,而是将写操作首先写入日志文件中,其次将写操作应用在memtable上。
当leveldb达到checkpoint点(memtable中的数据量超过了预设的阈值),会将当前memtable冻结成一个不可更改的内存数据库(immutablememory db),并且创建一个新的memtable供系统继续使用。
immutable memory db会在后台进行一次minorcompaction,即将内存数据库中的数据持久化到磁盘文件中。
注解
在这里我们暂时不展开讨论minorcompaction相关的内容,读者可以简单地理解为将内存中的数据持久化到文件
leveldb(或者说LSM树)设计Minor Compaction的目的是为了:
有效地降低内存的使用率;
避免日志文件过大,系统恢复时间过长;当memorydb的数据被持久化到文件中时,leveldb将以一定规则进行文件组织,这种文件格式成为sstable。在本文中将详细地介绍sstable的文件格式以及相关读写操作。