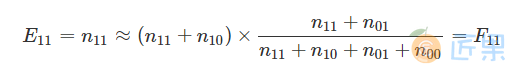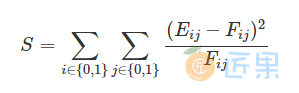四、练习_Pandas 教程

Ex1：缺失值与类别的相关性检验

在数据处理中，含有过多缺失值的列往往会被删除，除非缺失情况与标签强相关。下面有一份关于二分类问题的数据集，其中 X_1, X_2 为特征变量， y 为二分类标签。

In [97]: df = pd.read_csv('data/missing_chi.csv')
In [98]: df.head()
Out[98]: 
    X_1  X_2  y
0   NaN  NaN  0
1   NaN  NaN  0
2   NaN  NaN  0
3  43.0  NaN  0
4   NaN  NaN  0
In [99]: df.isna().mean()
Out[99]: 
X_1    0.855
X_2    0.894
y      0.000
dtype: float64
In [100]: df.y.value_counts(normalize=True)
Out[100]: 
0    0.918
1    0.082
Name: y, dtype: float64

事实上，有时缺失值出现或者不出现本身就是一种特征，并且在一些场合下可能与标签的正负是相关的。关于缺失出现与否和标签的正负性，在统计学中可以利用卡方检验来断言它们是否存在相关性。按照特征缺失的正例、特征缺失的负例、特征不缺失的正例、特征不缺失的负例，可以分为四种情况，设它们分别对应的样例数为 \( n_{11}, n_{10},n_{01},n_{00}\) 。假若它们是不相关的，那么特征缺失中正例的理论值，就应该接近于特征缺失总数 ×× 总体正例的比例，即：

其他的三种情况同理。现将实际值和理论值分别记作 Eij**,Fi****j**Eij,Fij ，那么希望下面的统计量越小越好，即代表实际值接近不相关情况的理论值：

可以证明上面的统计量近似服从自由度为 11 的卡方分布，即 \(S ~ X^2(1)\) 。因此，可通过计算 \( P(x^2(1)>S)\) 的概率来进行相关性的判别，一般认为当此概率小于 0.05 时缺失情况与标签正负存在相关关系，即不相关条件下的理论值与实际值相差较大。

上面所说的概率即为统计学上关于 2×2 列联表检验问题的 p 值，它可以通过 scipy.stats.chi2.sf(S, 1) 得到。请根据上面的材料，分别对 X_1, X_2 列进行检验。

Ex2：用回归模型解决分类问题

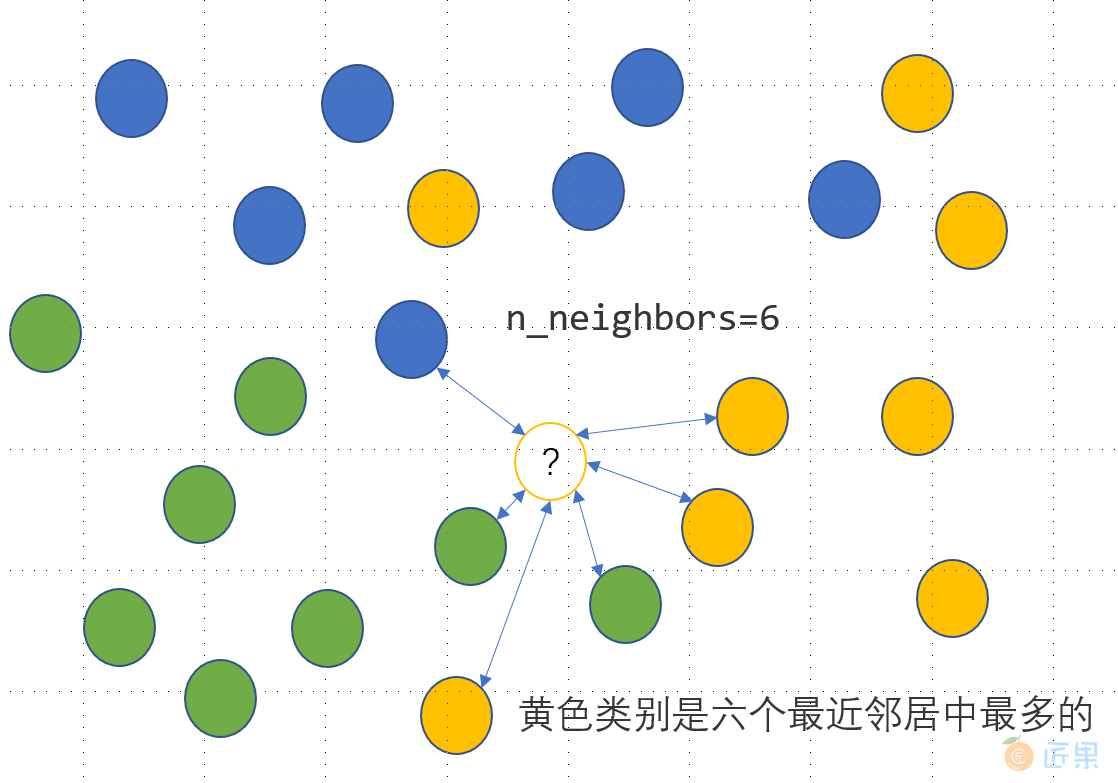
KNN 是一种监督式学习模型，既可以解决回归问题，又可以解决分类问题。对于分类变量，利用 KNN 分类模型可以实现其缺失值的插补，思路是度量缺失样本的特征与所有其他样本特征的距离，当给定了模型参数 n_neighbors=n 时，计算离该样本距离最近的 nn 个样本点中最多的那个类别，并把这个类别作为该样本的缺失预测类别，具体如下图所示，未知的类别被预测为黄色：

../_images/ch7_ex.png

上面有色点的特征数据提供如下：

In [101]: df = pd.read_excel('data/color.xlsx')
In [102]: df.head(3)
Out[102]: 
    X1   X2 Color
0 -2.5  2.8  Blue
1 -1.5  1.8  Blue
2 -0.8  2.8  Blue

已知待预测的样本点为 \( X_1 = 0.8, X_2 = -0.2\) ，那么预测类别可以如下写出：

In [103]: from sklearn.neighbors import KNeighborsClassifier
In [104]: clf = KNeighborsClassifier(n_neighbors=6)
In [105]: clf.fit(df.iloc[:,:2], df.Color)
Out[105]: KNeighborsClassifier(n_neighbors=6)
In [106]: clf.predict([[0.8, -0.2]])
Out[106]: array(['Yellow'], dtype=object)

对于回归问题而言，需要得到的是一个具体的数值，因此预测值由最近的 nn 个样本对应的平均值获得。请把上面的这个分类问题转化为回归问题，仅使用 KNeighborsRegressor 来完成上述的 KNeighborsClassifier 功能。
请根据第1问中的方法，对 audit 数据集中的 Employment 变量进行缺失值插补。

In [107]: df = pd.read_csv('data/audit.csv')
In [108]: df.head(3)
Out[108]: 
        ID  Age Employment    Marital     Income  Gender  Hours
0  1004641   38    Private  Unmarried   81838.00  Female     72
1  1010229   35    Private     Absent   72099.00    Male     30
2  1024587   32    Private   Divorced  154676.74    Male     40