上一节 的最后,笔者举例介绍了 Basic Paxos 的活锁问题,两个提案节点互不相让地争相提出自己的提案,抢占同一个值的修改权限,导致整个系统在持续性地“反复横跳”,外部看起来就像被锁住了一样。此外,笔者还讲述过一个观点,分布式共识的复杂性,主要来源于网络的不可靠与请求的可并发两大因素,活锁问题与许多 Basic Paxos 异常场景中所遭遇的麻烦,都可以看作是源于任何一个提案节点都能够完全平等地、与其他节点并发地提出提案而带来的复杂问题。为此,Lamport 专门设计(“专门设计”的意思是在 Paxos 的论文中 Lamport 随意提了几句可以这么做)了一种 Paxos 的改进版本“Multi Paxos”算法,希望能够找到一种两全其美的办法,既不破坏 Paxos 中“众节点平等”的原则,又能在提案节点中实现主次之分,限制每个节点都有不受控的提案权利,这两个目标听起来似乎是矛盾的,但现实世界中的选举就很符合这种在平等节点中挑选意见领袖的情景。
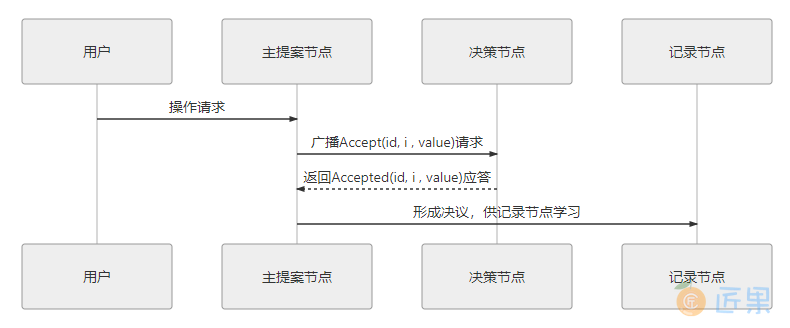
Multi Paxos 对 Basic Paxos 的核心改进是增加了“选主”的过程,提案节点会通过定时轮询(心跳),确定当前网络中的所有节点里是否存在有一个主提案节点,一旦没有发现主节点存在,节点就会在心跳超时后使用 Basic Paxos 中定义的准备、批准的两轮网络交互过程,向所有其他节点广播自己希望竞选主节点的请求,希望整个分布式系统对“由我作为主节点”这件事情协商达成一致共识,如果得到了决策节点中多数派的批准,便宣告竞选成功。当选主完成之后,除非主节点失联之后发起重新竞选,否则从此往后,就只有主节点本身才能够提出提案。此时,无论哪个提案节点接收到客户端的操作请求,都会将请求转发给主节点来完成提案,而主节点提案的时候,也就无需再次经过准备过程,因为可以视作是经过选举时的那一次准备之后,后续的提案都是对相同提案 ID 的一连串的批准过程。也可以通俗理解为选主过后,就不会再有其他节点与它竞争,相当于是处于无并发的环境当中进行的有序操作,所以此时系统中要对某个值达成一致,只需要进行一次批准的交互即可,如图 6-6 所示。
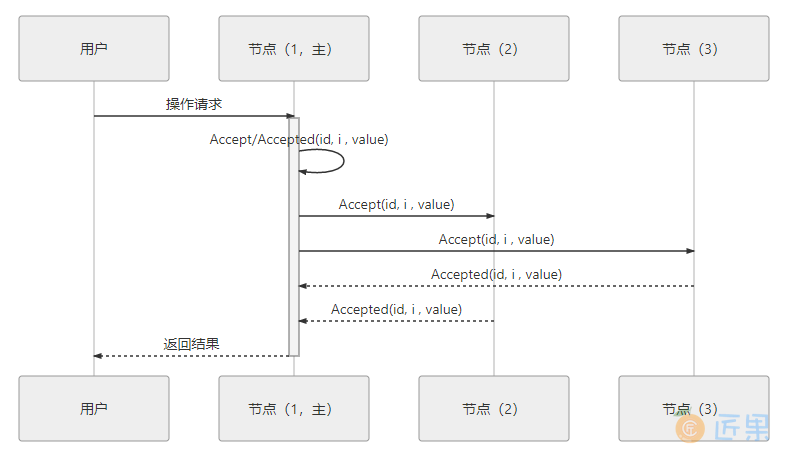
可能有人注意到这时候的二元组(id, value)已经变成了三元组(id, i, value),这是因为需要给主节点增加一个“任期编号”,这个编号必须是严格单调递增的,以应付主节点陷入网络分区后重新恢复,但另外一部分节点仍然有多数派,且已经完成了重新选主的情况,此时必须以任期编号大的主节点为准。当节点有了选主机制的支持,在整体来看,就可以进一步简化节点角色,不去区分提案、决策和记录节点了,统统以“节点”来代替,节点只有主(Leader)和从(Follower)的区别,此时协商共识的时序图如图 6-7 所示。
在这个理解的基础上,我们换一个角度来重新思考“分布式系统中如何对某个值达成一致”这个问题,可以把该问题划分做三个子问题来考虑,可以证明(具体证明就不列在这里了,感兴趣的读者可参考结尾给出的论文)当以下三个问题同时被解决时,即等价于达成共识:
- 如何选主(Leader Election)。
- 如何把数据复制到各个节点上(Entity Replication)。
- 如何保证过程是安全的(Safety)。
选主问题尽管还涉及许多工程上的细节,譬如心跳、随机超时、并行竞选,等等,但要只论原理的话,如果你已经理解了 Paxos 算法的操作步骤,相信对选主并不会有什么疑惑,因为这本质上仅仅是分布式系统对“谁来当主节点”这件事情的达成的共识而已,我们在前一节已经花了数千字来讲述分布式系统该如何对一件事情达成共识,这里就不重复赘述了,下面直接来解决数据(Paxos 中的提案、Raft 中的日志)在网络各节点间的复制问题。
在正常情况下,当客户端向主节点发起一个操作请求,譬如提出“将某个值设置为 X”,此时主节点将 X 写入自己的变更日志,但先不提交,接着把变更 X 的信息在下一次心跳包中广播给所有的从节点,并要求从节点回复确认收到的消息,从节点收到信息后,将操作写入自己的变更日志,然后给主节点发送确认签收的消息,主节点收到过半数的签收消息后,提交自己的变更、应答客户端并且给从节点广播可以提交的消息,从节点收到提交消息后提交自己的变更,数据在节点间的复制宣告完成。
在异常情况下,网络出现了分区,部分节点失联,但只要仍能正常工作的节点的数量能够满足多数派(过半数)的要求,分布式系统就仍然可以正常工作,这时候数据复制过程如下:
- 假设有 S~1~ 、S~2~ 、S~3~ 、S~4~ 、S~5~ 五个节点,S~1~ 是主节点,由于网络故障,导致 S~1~ 、S~2~ 和 S~3~ 、S~4~ 、S~5~ 之间彼此无法通信,形成网络分区。
- 一段时间后,S~3~ 、S~4~ 、S~5~ 三个节点中的某一个(譬如是 S~3~ )最先达到心跳超时的阈值,获知当前分区中已经不存在主节点了,它向所有节点发出自己要竞选的广播,并收到了 S~4~ 、S~5~ 节点的批准响应,加上自己一共三票,即得到了多数派的批准,竞选成功,此时系统中同时存在 S~1~ 和 S~3~ 两个主节点,但由于网络分区,它们不会知道对方的存在。
- 这种情况下,客户端发起操作请求:
- 如果客户端连接到了 S~1~ 、S~2~ 之一,都将由 S~1~ 处理,但由于操作只能获得最多两个节点的响应,不构成多数派的批准,所以任何变更都无法成功提交。
- 如果客户端连接到了 S~3~ 、S~4~ 、S~5~ 之一,都将由 S~3~ 处理,此时操作可以获得最多三个节点的响应,构成多数派的批准,是有效的,变更可以被提交,即系统可以继续提供服务。
- 事实上,以上两种“如果”情景很少机会能够并存。网络分区是由于软、硬件或者网络故障而导致的,内部网络出现了分区,但两个分区仍然能分别与外部网络的客户端正常通信的情况甚为少见。更多的场景是算法能容忍网络里下线了一部分节点,按照这个例子来说,如果下线了两个节点,系统正常工作,下线了三个节点,那剩余的两个节点也不可能继续提供服务了。
- 假设现在故障恢复,分区解除,五个节点可以重新通信了:
- S~1~ 和 S~3~ 都向所有节点发送心跳包,从各自的心跳中可以得知两个主节点里 S~3~ 的任期编号更大,它是最新的,此时五个节点均只承认 S~3~ 是唯一的主节点。
- S~1~ 、S~2~ 回滚它们所有未被提交的变更。
- S~1~ 、S~2~ 从主节点发送的心跳包中获得它们失联期间发生的所有变更,将变更提交写入本地磁盘。
- 此时分布式系统各节点的状态达成最终一致。
下面我们来看第三个问题:“如何保证过程是安全的”,不知你是否感觉到这个问题与前两点的存在一点差异?选主、数据复制都是很具体的行为,但是“安全”就很模糊,什么算是安全或者不安全?
在分布式理论中,Safety和Liveness两种属性是有预定义的术语,在专业的资料中一般翻译成“协定性”和“终止性”,这两个概念也是由 Lamport 最先提出,当时给出的定义是:
- 协定性(Safety):所有的坏事都不会发生(something "bad" will never happen)。
- 终止性(Liveness):所有的好事都终将发生,但不知道是啥时候(something "good" will must happen, but we don't know when)。
这种就算解释了你也看不明白的定义,是不是很符合 Lamport 老爷子一贯的写作风格?(笔者无奈地摊手苦笑)。我们不去纠结严谨的定义,仍通过举例来说明它们的具体含义。譬如以选主问题为例,Safety 保证了选主的结果一定是有且只有唯一的一个主节点,不可能同时出现两个主节点;而 Liveness 则要保证选主过程是一定可以在某个时刻能够结束的。由前面对活锁的介绍可以得知,在 Liveness 这个属性上选主问题是存在理论上的瑕疵的,可能会由于活锁而导致一直无法选出明确的主节点,所以 Raft 论文中只写了对 Safety 的保证,但由于工程实现上的处理,现实中是几乎不可能会出现终止性的问题。
最后,以上这种把共识问题分解为“Leader Election”、“Entity Replication”和“Safety”三个问题来思考、解决的解题思路,即“Raft 算法”,这篇以《一种可以让人理解的共识算法》(In Search of an Understandable Consensus Algorithm)为题的论文提出了 Raft 算法,并获得了 USENIX ATC 2014 大会的 Best Paper,后来更是成为 Etcd、LogCabin、Consul 等重要分布式程序的实现基础,ZooKeeper 的 ZAB 算法与 Raft 的思路也非常类似,这些算法都被认为是 Multi Paxos 的等价派生实现。