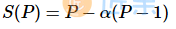并行编程的发展产生了对性能指标和并行程序评估软件的需求,通过评估性能才能确定该算法是否方便快捷。实际上,并行计算的重点是在相对较短的时间内解决体量较大的问题。为了能够达到这个目的,需要考虑的因素有:使用的硬件类型,问题的可并行程度和采用的编程模型等。为了加速算法评估过程,引进了基本概念分析,也就是将并行算法和原始的顺序执行做对比。通过分析和确定线程数量和/或使用的处理器数量来确定性能。
为了进行分析,在这里介绍几个性能指标:加速比,效率和扩展性。
阿姆德尔定律 (Ahmdal’s law) 引入了并行计算的极限,来评估串行算法并行化的效率。古斯塔夫森定律 (Gustafson’s law) 也做了相似的评估。
1. 加速比
加速比用于衡量使用并行方式解决问题的收益。假设使用单个处理单元解决这个问题需要的时间为 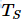
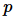

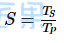
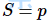
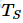
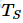
下面概括了上述的情况:
为线性加速比,也是理想加速比。
为真实加速比
为超线性加速比
2. 效率
在理想状态下,如果一个并行系统有 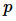
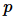
假设效率为 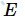
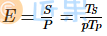
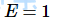
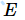
- 当
,为线性加速比。
- 当
,为真实情况。
- 当
,可以确定这是一个有问题的低效并行算法。
3. 伸缩性
伸缩性用于度量并行机器高效运行的能力,代表跟处理器数量成比例的计算能力 (执行速度)。如果问题的规模和处理器的数量同时增加,性能不会下降。在依靠各种因素叠加的可伸缩系统中,可以保持相同的效率或者有更高的效率。
4. 阿姆德尔定律 (Ahmdal’s law)
阿姆德尔定律广泛使用于处理器设计和并行算法设计。它指出程序能达到的最大加速比被程序的串行部分限制。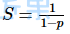
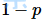
5. 古斯塔夫森定律 (Gustafson’s law)
古斯塔夫森定律在考虑下面的情况之后得出的:
- 当问题的规模增大时,程序的串行部分保持不变。
- 当增加处理器的数量时,每个处理器执行的任务仍然相同。
古斯塔夫森定律指出了加速比