范畴学

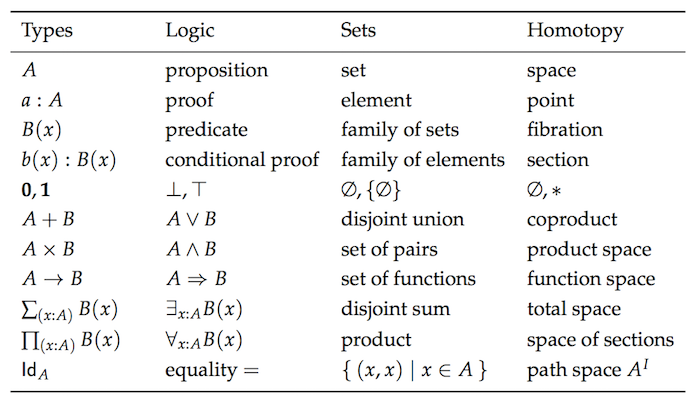
范畴学（category theory）是数学中的一个抽象分支，能够形式化诸如集合论（set theory）、类型论（type theory）、群论（group theory）以及逻辑学（logic）等数学分支中的一些概念。范畴学主要处理对象（object）、态射（morphism）和变化式（transformation），而这些概念跟编程的联系非常紧密。下图是一些相同的概念分别在不同理论下的形式：

抱歉，我没有任何要吓唬你的意思。我并不假设你对这些概念都了如指掌，我只是想让你明白这里面有多少重复的内容，让你知道为何范畴学要统一这些概念。

在范畴学中，有一个概念叫做...范畴。有着以下这些组件（component）的搜集（collection）就构成了一个范畴：

范畴学抽象到足以模拟任何事物，不过目前我们最关心的还是类型和函数，所以让我们把范畴学运用到它们身上看看。

对象的搜集

对象就是数据类型，例如 String、Boolean、Number 和 Object 等等。通常我们把数据类型视作所有可能的值的一个集合（set）。像 Boolean 就可以看作是 [true, false] 的集合，Number 可以是所有实数的一个集合。把类型当作集合对待是有好处的，因为我们可以利用集合论（set theory）处理类型。

态射的搜集

态射是标准的、普通的纯函数。

态射的组合

你可能猜到了，这就是本章介绍的新玩意儿——组合。我们已经讨论过 compose 函数是符合结合律的，这并非巧合，结合律是在范畴学中对任何组合都适用的一个特性。

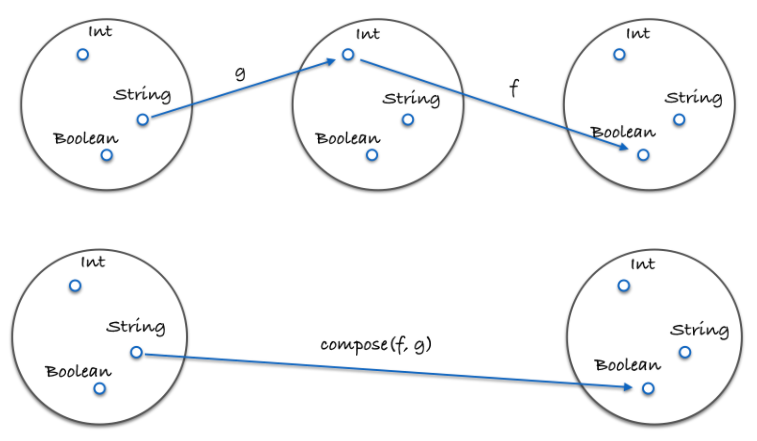
这张图展示了什么是组合：

这里有一个具体的例子：

var g = function(x){ return x.length; };
var f = function(x){ return x === 4; };
var isFourLetterWord = compose(f, g);

identity 这个独特的态射

让我们介绍一个名为 id 的实用函数。这个函数接受随便什么输入然后原封不动地返回它：

var id = function(x){ return x; };

你可能会问“这到底哪里有用了？”。别急，我们会在随后的章节中拓展这个函数的，暂时先把它当作一个可以替代给定值的函数——一个假装自己是普通数据的函数。

id 函数跟组合一起使用简直完美。下面这个特性对所有的一元函数（unary function）（一元函数：只接受一个参数的函数） f 都成立：

// identity
compose(id, f) == compose(f, id) == f;
// true

嘿，这就是实数的单位元（identity property）嘛！如果这还不够清楚直白，别着急，慢慢理解它的无用性。很快我们就会到处使用 id 了，不过暂时我们还是把它当作一个替代给定值的函数。这对写 pointfree 的代码非常有用。

好了，以上就是类型和函数的范畴。不过如果你是第一次听说这些概念，我估计你还是有些迷糊，不知道范畴到底是什么，为什么有用。没关系，本书全书都在借助这些知识编写示例代码。至于现在，就在本章，本行文字中，你至少可以认为它向我们提供了有关组合的知识——比如结合律和单位律。

除了类型和函数，还有什么范畴呢？还有很多，比如我们可以定义一个有向图（directed graph），以节点为对象，以边为态射，以路径连接为组合。还可以定义一个实数类型（Number），以所有的实数为对象，以 >= 为态射（实际上任何偏序（partial order）或全序（total order）都可以成为一个范畴）。范畴的总数是无限的，但是要达到本书的目的，我们只需要关心上面定义的范畴就好了。至此我们已经大致浏览了一些表面的东西，必须要继续后面的内容了。