我们要看的第一条定律是结合律,但可能不是你熟悉的那个结合律。
// 结合律
compose(join, map(join)) == compose(join, join)
这些定律表明了 monad 的嵌套本质,所以结合律关心的是如何让内层或外层的容器类型 join,然后取得同样的结果。用一张图来表示可能效果会更好:
从左上角往下,先用 join 合并 M(M(M a)) 最外层的两个 M,然后往右,再调用一次 join,就得到了我们想要的 M a。或者,从左上角往右,先打开最外层的 M,用 map(join) 合并内层的两个 M,然后再向下调用一次 join,也能得到 M a。不管是先合并内层还是先合并外层的 M,最后都会得到相同的 M a,所以这就是结合律。值得注意的一点是 map(join) != join。两种方式的中间步骤可能会有不同的值,但最后一个 join 调用后最终结果是一样的。
第二个定律与结合律类似:
// 同一律 (M a)
compose(join, of) == compose(join, map(of)) == id
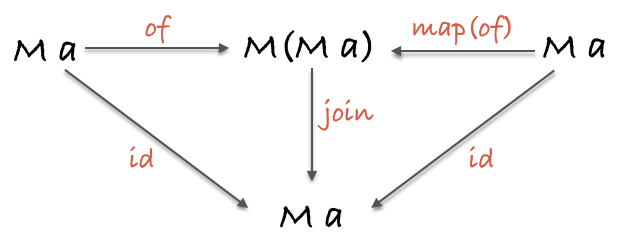
这表明,对任意的 monad M,of 和 join 相当于 id。也可以使用 map(of) 由内而外实现相同效果。我们把这个定律叫做“三角同一律”(triangle identity),因为把它图形化之后就像一个三角形:
如果从左上角开始往右,可以看到 of 的确把 M a 丢到另一个 M 容器里去了。然后再往下 join,就得到了 M a,跟一开始就调用 id 的结果一样。从右上角往左,可以看到如果我们通过 map 进到了 M 里面,然后对普通值 a 调用 of,最后得到的还是 M (M a);再调用一次 join 将会把我们带回原点,即 M a。
我要说明一点,尽管这里我写的是 of,实际上对任意的 monad 而言,都必须要使用明确的 M.of。
我已经见过这些定律了,同一律和结合律,以前就在哪儿见过...等一下,让我想想...是的!它们是范畴遵循的定律!不过这意味着我们需要一个组合函数来给出一个完整定义。见证吧:
var mcompose = function(f, g) {
return compose(chain(f), chain(g));
}
// 左同一律
mcompose(M, f) == f
// 右同一律
mcompose(f, M) == f
// 结合律
mcompose(mcompose(f, g), h) == mcompose(f, mcompose(g, h))
毕竟它们是范畴学里的定律。monad 来自于一个叫 “Kleisli 范畴”的范畴,这个范畴里边所有的对象都是 monad,所有的态射都是联结函数(chained funtions)。我不是要在没有提供太多解释的情况下,拿范畴学里各式各样的概念来取笑你。我的目的是涉及足够多的表面知识,向你说明这中间的相关性,让你在关注日常实用特性之余,激发起对这些定律的兴趣。