二叉查找树的树高度影响了查找的效率,需要尽量减小树的高度,AVL树正是这样的树。
一、AVL树介绍
AVL树是一棵严格自平衡的二叉查找树,1962年,发明者 Adelson-Velsky 和 Landis 发表了论文,以两个作者的名字命名了该数据结构,这是较早发明的平衡二叉树。定义如下:
- 首先它是一棵二叉查找树。
- 任意一个节点的左右子树最大高度差为1。
由于树特征定义,我们可以计算出其高度 h 的上界 h<=1.44log(n),也就是最坏情况下,树的高度约等于 1.44log(n)。
假设高度
h的AVL树最少有f(h)个节点,因为左右子树的高度差不能大于1,所以左子树和右子树最少节点为:f(h-1),f(h-2)。因此,树根节点加上左右子树的节点,满足公式
f(h) = 1 + f(h-1) + f(h-2),初始条件f(0)=0,f(1)=1。经过数学的推算可以得出 h<=1.44log(n),由于计算过程超纲了,在此不进行演算。
树的高度被限制于 1.44log(n), 所以查找元素时使用二分查找,最坏查找 1.44log(n) 次,此时最坏时间复杂度为 1.44log(n),去掉常数项,时间复杂度为:log(n)。
为了维持AVL树的特征,每次添加和删除元素都需要一次或多次旋转来调整树的平衡。调整的依据来自于二叉树节点的平衡因子:节点的左子树与右子树的高度差称为该节点的平衡因子,约束范围为 [-1,0,1]。
平衡二叉查找树比较难以理解的是添加和删除元素时的调整操作,我们将会具体分析。
二、AVL树基本结构
AVL树的数据结构如下:
// AVL树
type AVLTree struct {
Root *AVLTreeNode // 树根节点
}
// AVL节点
type AVLTreeNode struct {
Value int64 // 值
Times int64 // 值出现的次数
Height int64 // 该节点作为树根节点,树的高度,方便计算平衡因子
Left *AVLTreeNode // 左子树
Right *AVLTreeNode // 右字树
}
// 初始化一个AVL树
func NewAVLTree() *AVLTree {
return new(AVLTree)
}
其中 Height 表示以该节点作为树的根节点时该树的高度,方便计算平衡因子。更新树的高度,代码如下:
// 更新节点的树高度
func (node *AVLTreeNode) UpdateHeight() {
if node == nil {
return
}
var leftHeight, rightHeight int64 = 0, 0
if node.Left != nil {
leftHeight = node.Left.Height
}
if node.Right != nil {
rightHeight = node.Right.Height
}
// 哪个子树高算哪棵的
maxHeight := leftHeight
if rightHeight > maxHeight {
maxHeight = rightHeight
}
// 高度加上自己那一层
node.Height = maxHeight + 1
}
计算树的平衡因子,也就是左右子树的高度差,代码如下:
// 计算平衡因子
func (node *AVLTreeNode) BalanceFactor() int64 {
var leftHeight, rightHeight int64 = 0, 0
if node.Left != nil {
leftHeight = node.Left.Height
}
if node.Right != nil {
rightHeight = node.Right.Height
}
return leftHeight - rightHeight
}
三、AVL树添加元素
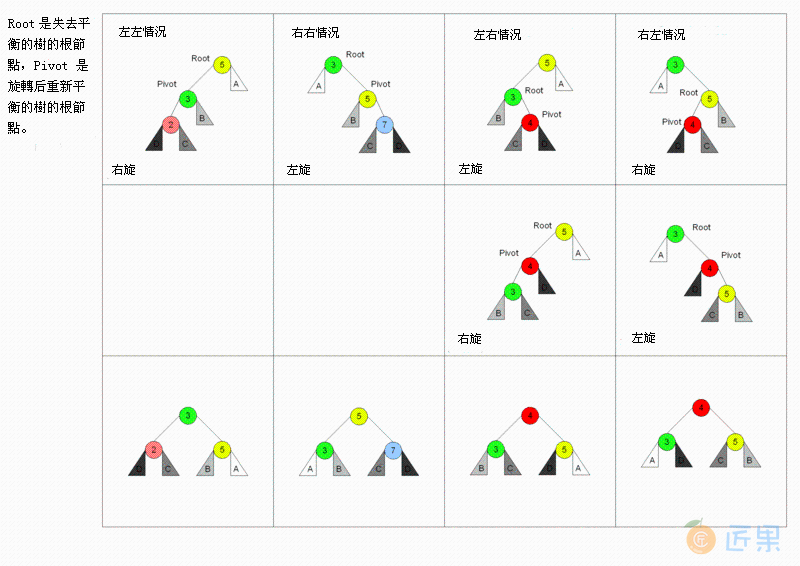
添加元素前需要定位到元素的位置,也就是使用二分查找找到该元素需要插入的地方。插入后,需要满足所有节点的平衡因子在 [-1,0,1] 范围内,如果不在,需要进行旋转调整。旋转有四种情况:
- 在右子树上插上右儿子导致失衡,左旋,转一次。
- 在左子树上插上左儿子导致失衡,右旋,转一次。
- 在左子树上插上右儿子导致失衡,先左后右旋,转两次。
- 在右子树上插上左儿子导致失衡,先右后左旋,转两次。
旋转规律记忆法:单旋和双旋,单旋反方向,双旋同方向。以下示意图摘自维基百科,阅读代码时可以参考。
3.1. 左子树插左儿子:单右旋
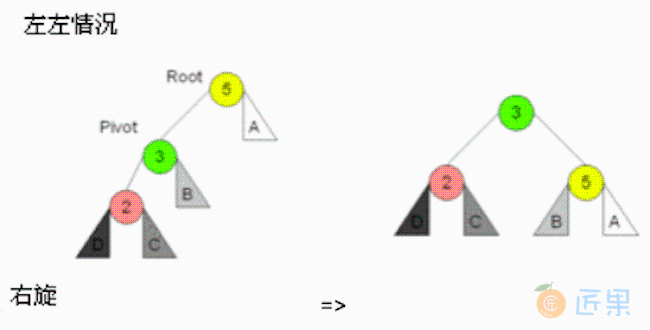
在左子树上插上左儿子导致失衡,需要单右旋:
因为红色元素 2 的产生,其最近的父亲节点 Root 失衡了,元素 2 导致了元素 Root=5 的失衡,需要调整。
将 Pivot=3 代替元素 5 的位置成为新的 Root,然后元素 5 委屈一下成为 3 的右儿子,而 3 的右儿子变成了 5 的左儿子,如上图。
相应调整后树的高度降低了,该失衡消失。我们可以看到红色元素 2 有两个儿子,实际上在添加操作时它是一个新的节点,是没有儿子的,这种有儿子的情况只发生在删除操作。
如果一时难以理解,可以多看几次图好好思考。代码如下:
// 单右旋操作,看图说话
func RightRotation(Root *AVLTreeNode) *AVLTreeNode {
// 只有Pivot和B,Root位置变了
Pivot := Root.Left
B := Pivot.Right
Pivot.Right = Root
Root.Left = B
// 只有Root和Pivot变化了高度
Root.UpdateHeight()
Pivot.UpdateHeight()
return Pivot
}
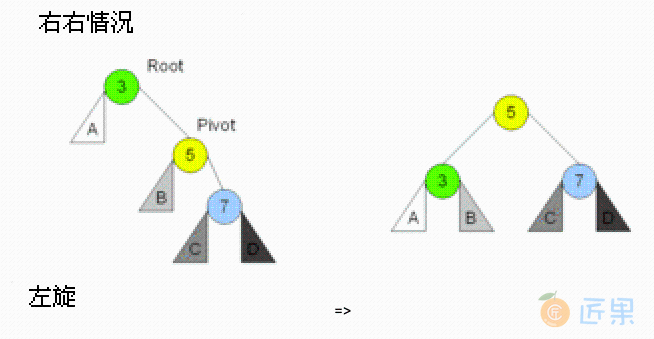
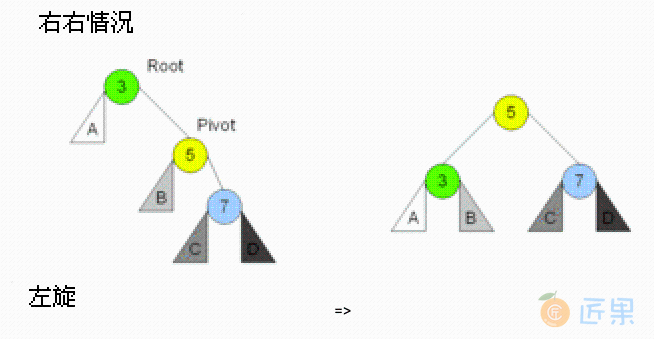
3.2. 右子树插右儿子:单左旋
在右子树上插上右儿子导致失衡,需要单左旋:
代码如下:
// 单左旋操作,看图说话
func LeftRotation(Root *AVLTreeNode) *AVLTreeNode {
// 只有Pivot和B,Root位置变了
Pivot := Root.Right
B := Pivot.Left
Pivot.Left = Root
Root.Right = B
// 只有Root和Pivot变化了高度
Root.UpdateHeight()
Pivot.UpdateHeight()
return Pivot
}
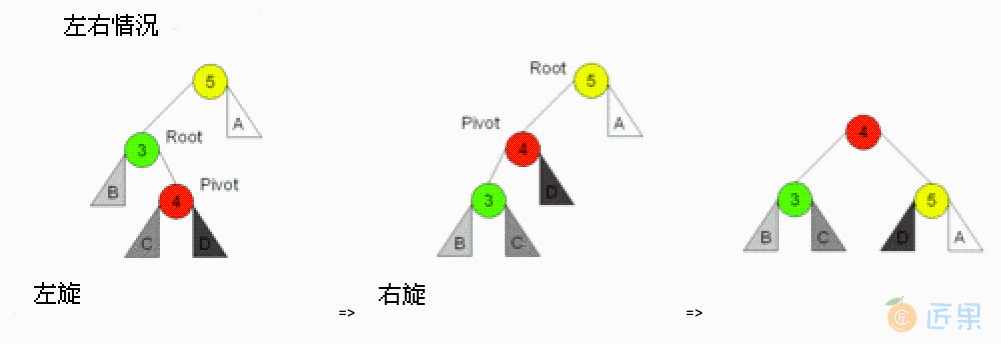
3.3. 左子树插右儿子:先左后右旋
在左子树上插上右儿子导致失衡,先左后右旋:
代码如下:
// 先左后右旋操作,看图说话
func LeftRightRotation(node *AVLTreeNode) *AVLTreeNode {
node.Left = LeftRotation(node.Left)
return RightRotation(node)
}
直接复用了之前左旋和右旋的代码,虽然难以理解,但是画一下图,确实这样调整后树高度降了,不再失衡,一切 perfect。
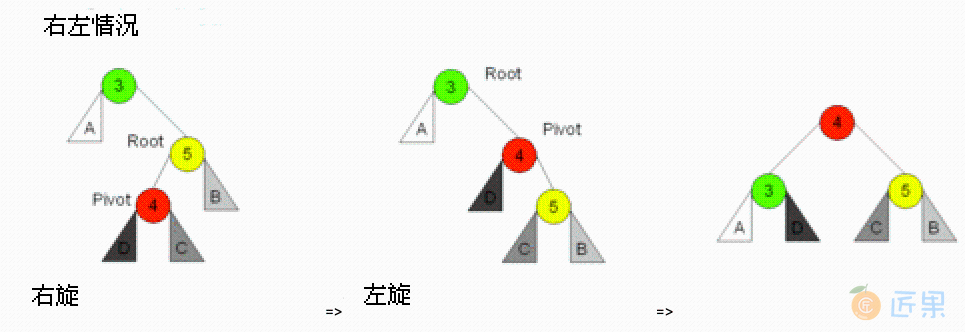
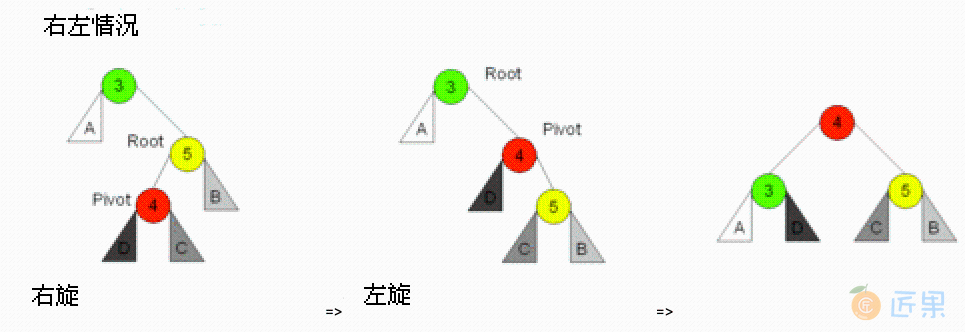
3.4. 右子树插左儿子:先右后左旋
在右子树上插上左儿子导致失衡,先右后左旋:
代码如下:
// 先右后左旋操作,看图说话
func RightLeftRotation(node *AVLTreeNode) *AVLTreeNode {
node.Right = RightRotation(node.Right)
return LeftRotation(node)
}
3.5. 具体实现
四种旋转代码实现后,我们开始进行添加元素操作:
// 添加元素
func (tree *AVLTree) Add(value int64) {
// 往树根添加元素,会返回新的树根
tree.Root = tree.Root.Add(value)
}
func (node *AVLTreeNode) Add(value int64) *AVLTreeNode {
// 添加值到根节点node,如果node为空,那么让值成为新的根节点,树的高度为1
if node == nil {
return &AVLTreeNode{Value: value, Height: 1}
}
// 如果值重复,什么都不用做,直接更新次数
if node.Value == value {
node.Times = node.Times + 1
return node
}
// 辅助变量
var newTreeNode *AVLTreeNode
if value > node.Value {
// 插入的值大于节点值,要从右子树继续插入
node.Right = node.Right.Add(value)
// 平衡因子,插入右子树后,要确保树根左子树的高度不能比右子树低一层。
factor := node.BalanceFactor()
// 右子树的高度变高了,导致左子树-右子树的高度从-1变成了-2。
if factor == -2 {
if value > node.Right.Value {
// 表示在右子树上插上右儿子导致失衡,需要单左旋:
newTreeNode = LeftRotation(node)
} else {
//表示在右子树上插上左儿子导致失衡,先右后左旋:
newTreeNode = RightLeftRotation(node)
}
}
} else {
// 插入的值小于节点值,要从左子树继续插入
node.Left = node.Left.Add(value)
// 平衡因子,插入左子树后,要确保树根左子树的高度不能比右子树高一层。
factor := node.BalanceFactor()
// 左子树的高度变高了,导致左子树-右子树的高度从1变成了2。
if factor == 2 {
if value < node.Left.Value {
// 表示在左子树上插上左儿子导致失衡,需要单右旋:
newTreeNode = RightRotation(node)
} else {
//表示在左子树上插上右儿子导致失衡,先左后右旋:
newTreeNode = LeftRightRotation(node)
}
}
}
if newTreeNode == nil {
// 表示什么旋转都没有,根节点没变,直接刷新树高度
node.UpdateHeight()
return node
} else {
// 旋转了,树根节点变了,需要刷新新的树根高度
newTreeNode.UpdateHeight()
return newTreeNode
}
}
一开始从树根节点开始插入新值:tree.Root = tree.Root.Add(value),因为插入值后会返回新的根节点,也就是说调整过程中树根节点会变化,所以要重新将新根节点赋予老的根节点。
在 func (node *AVLTreeNode) Add(value int64) 函数中,如果根节点为空,那么需要返回新的根节点:
// 添加值到根节点node,如果node为空,那么让值成为新的根节点,树的高度为1
if node == nil {
return &AVLTreeNode{Value: value, Height: 1}
}
接着,如果插入的值和节点的值一样,直接更新 Times:
// 如果值重复,什么都不用做,直接更新次数
if node.Value == value {
node.Times = node.Times + 1
return node
}
否则根据值的大小,旋转插入到左子树或右子树,我们只分析插入右子树的代码:
if value > node.Value {
// 插入的值大于节点值,要从右子树继续插入
node.Right = node.Right.Add(value)
// 平衡因子,插入右子树后,要确保树根左子树的高度不能比右子树低一层。
factor := node.BalanceFactor()
// 右子树的高度变高了,导致左子树-右子树的高度从-1变成了-2。
if factor == -2 {
if value > node.Right.Value {
// 表示在右子树上插上右儿子导致失衡,需要单左旋:
newTreeNode = LeftRotation(node)
} else {
//表示在右子树上插上左儿子导致失衡,先右后左旋:
newTreeNode = RightLeftRotation(node)
}
}
}
因为值添加到了右子树,所以转换成了在右子树添加元素:node.Right = node.Right.Add(value),之后要判断根节点的平衡因子是否变化了。
值插入右子树后,要确保树根左子树的高度不能比右子树低一层。当平衡因子 factor == -2 表示右子树的高度变高了,导致 左子树-右子树 的高度从 -1 变成了 -2,所以要旋转。判断新插入的值是在右子树的左儿子还是右儿子上:
if value > node.Right.Value {
// 表示在右子树上插上右儿子导致失衡,需要单左旋:
newTreeNode = LeftRotation(node)
} else {
//表示在右子树上插上左儿子导致失衡,先右后左旋:
newTreeNode = RightLeftRotation(node)
}
如果在右子树上插上右儿子导致失衡,需要单左旋:LeftRotation(node),如果在右子树上插上左儿子导致失衡,先右后左旋:RightLeftRotation(node)。
最后需要更新树根节点的高度,并返回树根(如果曾经旋转,表示树根变了,需要返回新的树根):
if newTreeNode == nil {
// 表示什么旋转都没有,根节点没变,直接刷新树高度
node.UpdateHeight()
return node
} else {
// 旋转了,树根节点变了,需要刷新新的树根高度
newTreeNode.UpdateHeight()
return newTreeNode
}
3.6. 时间复杂度分析
添加元素时先要找到元素插入的位置,找到位置后逐层自底向上更新每个子树的树高度,并根据子树平衡是否被破坏,需要进行旋转操作。
由于树的高度最高为 1.44log(n),查找元素插入位置,最坏次数为 1.44log(n) 次。逐层更新子树高度并判断平衡是否被破坏,最坏需要 1.44log(n) 次,因此可以得知添加元素最坏时间复杂度为:2.88log(n),去掉常数项,时间复杂度为:log(n)。
关于旋转次数,当插入节点后,某子树不平衡时最多旋转 2次,也就是双旋该子树即可恢复平衡,该调整为局部特征,调整完后其父层不再需要旋转。也就是说,插入操作最坏旋转两次即可。
由于代码的递归实现方式,当某子树旋转过后其父层子树仍然需要判断平衡因子,判断是否需要旋转,该操作是不必要的,因为子树旋转过后全局已经平衡了,不必再判断父层的平衡因子。
对此可以进行代码优化,在左子树或右子树插入元素后,除了返回根节点,还返回其是否旋转过的辅助变量,如:func (node *AVLTreeNode) Add(value int64) (newNode *AVLTreeNode, rotate bool) ,根据返回的辅助变量 rotate,可以:
node.Right, rotate= node.Right.Add(value)
if !rotate {
// 子树没有旋转过,那么需要判断是否需要旋转
// 平衡因子,插入右子树后,要确保树根左子树的高度不能比右子树低一层。
factor := node.BalanceFactor()
// 右子树的高度变高了,导致左子树-右子树的高度从-1变成了-2。
if factor == -2 {
if value > node.Right.Value {
// 表示在右子树上插上右儿子导致失衡,需要单左旋:
newTreeNode = LeftRotation(node)
} else {
//表示在右子树上插上左儿子导致失衡,先右后左旋:
newTreeNode = RightLeftRotation(node)
}
}
}else{
// do nothing
}
但此优化意义不大,因为返回辅助变量后仍然需要判断,判断辅助变量和判断平衡因子,时间复杂度一样。
插入元素进行调整后,需要递归向上更新每一棵子树高度,其时间复杂度为 log(n),但可以优化,当两棵子树高度都没有变化时,那么上面的父层子树们都不需要更新树高度,直接退出,由于是递归程序,如何向上传递这个信息,引入了额外空间成本,且不可避免仍然会出现所有层级的父节点都必须更新树高度,优化意义不是很大。
四、AVL树查找元素等操作
其他操作与二叉查找树通用,代码如下:
// 找出最小值的节点
func (tree *AVLTree) FindMinValue() *AVLTreeNode {
if tree.Root == nil {
// 如果是空树,返回空
return nil
}
return tree.Root.FindMinValue()
}
func (node *AVLTreeNode) FindMinValue() *AVLTreeNode {
// 左子树为空,表面已经是最左的节点了,该值就是最小值
if node.Left == nil {
return node
}
// 一直左子树递归
return node.Left.FindMinValue()
}
// 找出最大值的节点
func (tree *AVLTree) FindMaxValue() *AVLTreeNode {
if tree.Root == nil {
// 如果是空树,返回空
return nil
}
return tree.Root.FindMaxValue()
}
func (node *AVLTreeNode) FindMaxValue() *AVLTreeNode {
// 右子树为空,表面已经是最右的节点了,该值就是最大值
if node.Right == nil {
return node
}
// 一直右子树递归
return node.Right.FindMaxValue()
}
// 查找指定节点
func (tree *AVLTree) Find(value int64) *AVLTreeNode {
if tree.Root == nil {
// 如果是空树,返回空
return nil
}
return tree.Root.Find(value)
}
func (node *AVLTreeNode) Find(value int64) *AVLTreeNode {
if value == node.Value {
// 如果该节点刚刚等于该值,那么返回该节点
return node
} else if value < node.Value {
// 如果查找的值小于节点值,从节点的左子树开始找
if node.Left == nil {
// 左子树为空,表示找不到该值了,返回nil
return nil
}
return node.Left.Find(value)
} else {
// 如果查找的值大于节点值,从节点的右子树开始找
if node.Right == nil {
// 右子树为空,表示找不到该值了,返回nil
return nil
}
return node.Right.Find(value)
}
}
// 中序遍历
func (tree *AVLTree) MidOrder() {
tree.Root.MidOrder()
}
func (node *AVLTreeNode) MidOrder() {
if node == nil {
return
}
// 先打印左子树
node.Left.MidOrder()
// 按照次数打印根节点
for i := 0; i <= int(node.Times); i++ {
fmt.Println(node.Value)
}
// 打印右子树
node.Right.MidOrder()
}
查找操作逻辑与通用的二叉查找树一样,并无区别。
五、AVL树删除元素
删除元素有四种情况:
- 删除的节点是叶子节点,没有儿子,直接删除后看离它最近的父亲节点是否失衡,做调整操作。
- 删除的节点下有两个子树,选择高度更高的子树下的节点来替换被删除的节点,如果左子树更高,选择左子树中最大的节点,也就是左子树最右边的叶子节点,如果右子树更高,选择右子树中最小的节点,也就是右子树最左边的叶子节点。最后,删除这个叶子节点,也就是变成情况1。
- 删除的节点只有左子树,可以知道左子树其实就只有一个节点,被删除节点本身(假设左子树多于2个节点,那么高度差就等于2了,不符合AVL树定义),将左节点替换被删除的节点,最后删除这个左节点,变成情况1。
- 删除的节点只有右子树,可以知道右子树其实就只有一个节点,被删除节点本身(假设右子树多于2个节点,那么高度差就等于2了,不符合AVL树定义),将右节点替换被删除的节点,最后删除这个右节点,变成情况1。
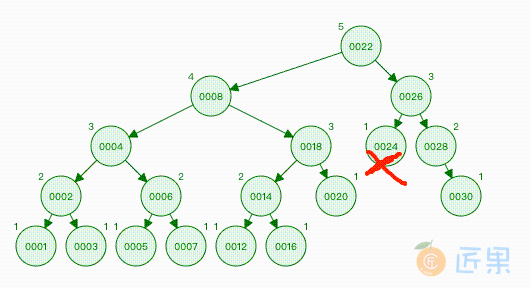
后面三种情况最后都变成 情况1,就是将删除的节点变成叶子节点,然后可以直接删除该叶子节点,然后看其最近的父亲节点是否失衡,失衡时对树进行平衡。举个例子,删除叶子节点,如图:
删除节点 24,导致节点 26 的子树不平衡了,这时需要对该子树进行旋转,旋转后如图:
可以发现这时树仍然不平衡,这时是节点 22 的子树不平衡,需要继续旋转,旋转后如图:
实现代码如下:
func (node *AVLTreeNode) Delete(value int64) *AVLTreeNode {
if node == nil {
// 如果是空树,直接返回
return nil
}
if value < node.Value {
// 从左子树开始删除
node.Left = node.Left.Delete(value)
// 删除后要更新该子树高度
node.Left.UpdateHeight()
} else if value > node.Value {
// 从右子树开始删除
node.Right = node.Right.Delete(value)
// 删除后要更新该子树高度
node.Right.UpdateHeight()
} else {
// 找到该值对应的节点
// 该节点没有左右子树
// 第一种情况,删除的节点没有儿子,直接删除即可。
if node.Left == nil && node.Right == nil {
return nil // 直接返回nil,表示直接该值删除
}
// 该节点有两棵子树,选择更高的哪个来替换
// 第二种情况,删除的节点下有两个子树,选择高度更高的子树下的节点来替换被删除的节点,如果左子树更高,选择左子树中最大的节点,也就是左子树最右边的叶子节点,如果右子树更高,选择右子树中最小的节点,也就是右子树最左边的叶子节点。最后,删除这个叶子节点。
if node.Left != nil && node.Right != nil {
// 左子树更高,拿左子树中最大值的节点替换
if node.Left.Height > node.Right.Height {
maxNode := node.Left
for maxNode.Right != nil {
maxNode = maxNode.Right
}
// 最大值的节点替换被删除节点
node.Value = maxNode.Value
node.Times = maxNode.Times
// 把最大的节点删掉
node.Left = node.Left.Delete(maxNode.Value)
// 删除后要更新该子树高度
node.Left.UpdateHeight()
} else {
// 右子树更高,拿右子树中最小值的节点替换
minNode := node.Right
for minNode.Left != nil {
minNode = minNode.Left
}
// 最小值的节点替换被删除节点
node.Value = minNode.Value
node.Times = minNode.Times
// 把最小的节点删掉
node.Right = node.Right.Delete(minNode.Value)
// 删除后要更新该子树高度
node.Right.UpdateHeight()
}
} else {
// 只有左子树或只有右子树
// 只有一个子树,该子树也只是一个节点,将该节点替换被删除的节点,然后置子树为空
if node.Left != nil {
//第三种情况,删除的节点只有左子树,因为树的特征,可以知道左子树其实就只有一个节点,它本身,否则高度差就等于2了。
node.Value = node.Left.Value
node.Times = node.Left.Times
node.Height = 1
node.Left = nil
} else if node.Right != nil {
//第四种情况,删除的节点只有右子树,因为树的特征,可以知道右子树其实就只有一个节点,它本身,否则高度差就等于2了。
node.Value = node.Right.Value
node.Times = node.Right.Times
node.Height = 1
node.Right = nil
}
}
// 找到值后,进行替换删除后,直接返回该节点
return node
}
// 左右子树递归删除节点后需要平衡
var newNode *AVLTreeNode
// 相当删除了右子树的节点,左边比右边高了,不平衡
if node.BalanceFactor() == 2 {
if node.Left.BalanceFactor() >= 0 {
newNode = RightRotation(node)
} else {
newNode = LeftRightRotation(node)
}
// 相当删除了左子树的节点,右边比左边高了,不平衡
} else if node.BalanceFactor() == -2 {
if node.Right.BalanceFactor() <= 0 {
newNode = LeftRotation(node)
} else {
newNode = RightLeftRotation(node)
}
}
if newNode == nil {
node.UpdateHeight()
return node
} else {
newNode.UpdateHeight()
return newNode
}
}
当删除的值不等于当前节点的值时,在相应的子树中递归删除,递归过程中会自底向上维护AVL树的特征。
- 小于删除的值
value < node.Value,在左子树中递归删除:node.Left = node.Left.Delete(value)。 - 大于删除的值
value > node.Value,在右子树中递归删除:node.Right = node.Right.Delete(value)。
因为删除后可能因为旋转调整,导致树根节点变了,这时会返回新的树根,递归删除后需要将返回的新根节点赋予原来的老根节点。
情况1,找到要删除的值时,该值是叶子节点,直接删除该节点即可:
// 第一种情况,删除的节点没有儿子,直接删除即可。
if node.Left == nil && node.Right == nil {
return nil // 直接返回nil,表示直接该值删除
}
情况2,删除的节点有两棵子树,选择高度更高的子树下的节点来替换被删除的节点:
// 该节点有两棵子树,选择更高的哪个来替换
// 第二种情况,删除的节点下有两个子树,选择高度更高的子树下的节点来替换被删除的节点,如果左子树更高,选择左子树中最大的节点,也就是左子树最右边的叶子节点,如果右子树更高,选择右子树中最小的节点,也就是右子树最左边的叶子节点。最后,删除这个叶子节点。
if node.Left != nil && node.Right != nil {
// 左子树更高,拿左子树中最大值的节点替换
if node.Left.Height > node.Right.Height {
maxNode := node.Left
for maxNode.Right != nil {
maxNode = maxNode.Right
}
// 最大值的节点替换被删除节点
node.Value = maxNode.Value
node.Times = maxNode.Times
// 把最大的节点删掉
node.Left = node.Left.Delete(maxNode.Value)
// 删除后要更新该子树高度
node.Left.UpdateHeight()
} else {
// 右子树更高,拿右子树中最小值的节点替换
minNode := node.Right
for minNode.Left != nil {
minNode = minNode.Left
}
// 最小值的节点替换被删除节点
node.Value = minNode.Value
node.Times = minNode.Times
// 把最小的节点删掉
node.Right = node.Right.Delete(minNode.Value)
// 删除后要更新该子树高度
node.Right.UpdateHeight()
}
}
情况3和情况4,如果被删除的节点只有一个子树,那么该子树一定没有儿子,不然树的高度就大于1了,所以直接替换值后删除该子树节点:
// 只有左子树或只有右子树
// 只有一个子树,该子树也只是一个节点,将该节点替换被删除的节点,然后置子树为空
if node.Left != nil {
//第三种情况,删除的节点只有左子树,因为树的特征,可以知道左子树其实就只有一个节点,它本身,否则高度差就等于2了。
node.Value = node.Left.Value
node.Times = node.Left.Times
node.Height = 1
node.Left = nil
} else if node.Right != nil {
//第四种情况,删除的节点只有右子树,因为树的特征,可以知道右子树其实就只有一个节点,它本身,否则高度差就等于2了。
node.Value = node.Right.Value
node.Times = node.Right.Times
node.Height = 1
node.Right = nil
}
核心在于删除后的旋转调整,如果删除的值不匹配当前节点的值,对当前节点的左右子树进行递归删除,递归删除后该节点为根节点的子树可能不平衡,我们需要判断后决定要不要旋转这棵树。
每次递归都是自底向上,从很小的子树到很大的子树,如果自底向上每棵子树都进行调整,约束在树的高度差不超过1,那么整棵树自然也符合AVL树的平衡规则。
删除元素后,如果子树失衡,需要进行调整操作,主要有两种:删除后左子树比右子树高,删除后右子树比左子树高。
5.1. 删除后,左子树比右子树高
如果删除了右子树的节点,左边比右边高了,不平衡了:
// 相当删除了右子树的节点,左边比右边高了,不平衡
if node.BalanceFactor() == 2 {
if node.Left.BalanceFactor() >= 0 {
newNode = RightRotation(node)
} else {
newNode = LeftRightRotation(node)
}
}
为什么要这么调整呢,看图说话,有两幅图参考:
这幅图可以看到:
黄色点5.BalanceFactor() == 2,对应:node.BalanceFactor() == 2。绿色点3.BalanceFactor() == 1,对应:node.Left.BalanceFactor() == 1。
所以应该需要右旋:newNode = RightRotation(node)
这幅图可以看到:
黄色点5.BalanceFactor() == 2,对应:node.BalanceFactor() == 2绿色点3.BalanceFactor() == -1,对应:node.Left.BalanceFactor() == -1。
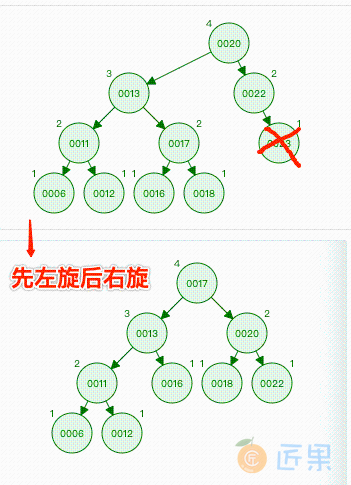
所以应该需要先左后右旋:newNode = LeftRightRotation(node)。还有一种特殊情况,和上面的都不一样,如图:
我们如果删除节点 22 或节点 23,这个时候根节点 20 失衡了。
- 根节点
20的左子树比右子树高了2层,对应:node.BalanceFactor() == 2。 - 左子树节点
13并没有失衡,对应:node.BalanceFactor() == 0。
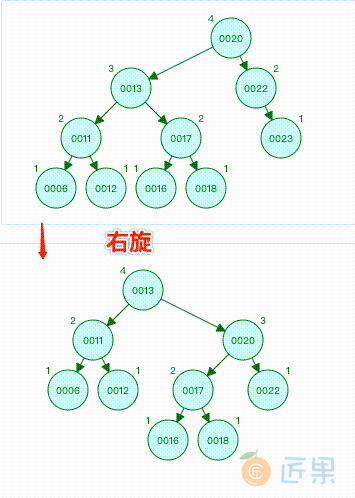
这个时候,无论使用右旋,还是先左旋后右旋都可以使树恢复平衡,我们的 if 判断条件使用了右旋。如果是先左旋后右旋,那么旋转后恢复平衡,如图对根结点进行旋转:
如果使用右旋也可以,如图对根结点进行旋转:
5.2. 删除后,右子树比左子树高
如果删除了左子树的节点,右边比左边高了,不平衡了:
// 相当删除了左子树的节点,右边比左边高了,不平衡
if node.BalanceFactor() == -2 {
if node.Right.BalanceFactor() <= 0 {
newNode = LeftRotation(node)
} else {
newNode = RightLeftRotation(node)
}
}
为什么要这么调整呢,看图说话,有两幅图参考:
这幅图可以看到:
绿色点3.BalanceFactor() == -2,对应:node.BalanceFactor() == -2。黄色点5.BalanceFactor() == -1,对应:node.Left.BalanceFactor() == -1。
所以应该需要左旋:newNode = LeftRotation(node)
这幅图可以看到:
绿色点3.BalanceFactor() == -2,对应:node.BalanceFactor() == -2。黄色点5.BalanceFactor() == 1,对应:node.Left.BalanceFactor() == 1。
所以应该需要先右后左旋:newNode = RightLeftRotation(node)。当然,还有另外一种特殊情况,与 5.1 章节类似,使用左旋还是先右旋后左旋都可以,在这里就不阐述了。
5.3. 删除后,调整树高度
进行调整操作后,需要更新该子树的高度。如果没有旋转过,更新之前节点的树高度。如果曾经旋转过,树根变了,更新新的树根节点高度。
if newNode == nil {
node.UpdateHeight()
return node
} else {
newNode.UpdateHeight()
return newNode
}
5.4. 时间复杂度分析
删除操作是先找到删除的节点,然后将该节点与一个叶子节点交换,接着删除叶子节点,最后对叶子节点的父层逐层向上旋转调整。
删除操作的时间复杂度和添加操作一样。区别在于,添加操作最多旋转两次就可以达到树的平衡,而删除操作可能会旋转超过两次。
如图是一棵比较糟糕的 AVL 树:
删除节点1,旋转可以一直旋转到根节点,比插入旋转最多旋转两次的次数更多。
六、验证是否是一棵AVL树
如何确保我们的代码实现的就是一棵 AVL 树呢,可以进行验证:
// 验证是不是棵AVL树
func (tree *AVLTree) IsAVLTree() bool {
if tree == nil || tree.Root == nil {
return true
}
// 判断节点是否符合 AVL 树的定义
if tree.Root.IsRight() {
return true
}
return false
}
// 判断节点是否符合 AVL 树的定义
func (node *AVLTreeNode) IsRight() bool {
if node == nil {
return true
}
// 左右子树都为空,那么是叶子节点
if node.Left == nil && node.Right == nil {
// 叶子节点高度应该为1
if node.Height == 1 {
return true
} else {
fmt.Println("leaf node height is ", node.Height)
return false
}
} else if node.Left != nil && node.Right != nil {
// 左右子树都是满的
// 左儿子必须比父亲小,右儿子必须比父亲大
if node.Left.Value < node.Value && node.Right.Value > node.Value {
} else {
// 不符合 AVL 树定义
fmt.Printf("father is %v lchild is %v, rchild is %v\n", node.Value, node.Left.Value, node.Right.Value)
return false
}
bal := node.Left.Height - node.Right.Height
if bal < 0 {
bal = -bal
}
// 子树高度差不能大于1
if bal > 1 {
fmt.Println("sub tree height bal is ", bal)
return false
}
// 如果左子树比右子树高,那么父亲的高度等于左子树+1
if node.Left.Height > node.Right.Height {
if node.Height == node.Left.Height+1 {
} else {
fmt.Printf("%#v height:%v,left sub tree height: %v,right sub tree height:%v\n", node, node.Height, node.Left.Height, node.Right.Height)
return false
}
} else {
// 如果右子树比左子树高,那么父亲的高度等于右子树+1
if node.Height == node.Right.Height+1 {
} else {
fmt.Printf("%#v height:%v,left sub tree height: %v,right sub tree height:%v\n", node, node.Height, node.Left.Height, node.Right.Height)
return false
}
}
// 递归判断子树
if !node.Left.IsRight() {
return false
}
// 递归判断子树
if !node.Right.IsRight() {
return false
}
} else {
// 只存在一棵子树
if node.Right != nil {
// 子树高度只能是1
if node.Right.Height == 1 && node.Right.Left == nil && node.Right.Right == nil {
if node.Right.Value > node.Value {
// 右节点必须比父亲大
} else {
fmt.Printf("%v,(%#v,%#v) child", node.Value, node.Right, node.Left)
return false
}
} else {
fmt.Printf("%v,(%#v,%#v) child", node.Value, node.Right, node.Left)
return false
}
} else {
if node.Left.Height == 1 && node.Left.Left == nil && node.Left.Right == nil {
if node.Left.Value < node.Value {
// 左节点必须比父亲小
} else {
fmt.Printf("%v,(%#v,%#v) child", node.Value, node.Right, node.Left)
return false
}
} else {
fmt.Printf("%v,(%#v,%#v) child", node.Value, node.Right, node.Left)
return false
}
}
}
return true
}
运行请看完整代码。
七、AVL树完整代码
package main
import (
"fmt"
)
// AVL树
type AVLTree struct {
Root *AVLTreeNode // 树根节点
}
// AVL节点
type AVLTreeNode struct {
Value int64 // 值
Times int64 // 值出现的次数
Height int64 // 该节点作为树根节点,树的高度,方便计算平衡因子
Left *AVLTreeNode // 左子树
Right *AVLTreeNode // 右字树
}
// 初始化一个AVL树
func NewAVLTree() *AVLTree {
return new(AVLTree)
}
// 更新节点的树高度
func (node *AVLTreeNode) UpdateHeight() {
if node == nil {
return
}
var leftHeight, rightHeight int64 = 0, 0
if node.Left != nil {
leftHeight = node.Left.Height
}
if node.Right != nil {
rightHeight = node.Right.Height
}
// 哪个子树高算哪棵的
maxHeight := leftHeight
if rightHeight > maxHeight {
maxHeight = rightHeight
}
// 高度加上自己那一层
node.Height = maxHeight + 1
}
// 计算平衡因子
func (node *AVLTreeNode) BalanceFactor() int64 {
var leftHeight, rightHeight int64 = 0, 0
if node.Left != nil {
leftHeight = node.Left.Height
}
if node.Right != nil {
rightHeight = node.Right.Height
}
return leftHeight - rightHeight
}
// 单右旋操作,看图说话
func RightRotation(Root *AVLTreeNode) *AVLTreeNode {
// 只有Pivot和B,Root位置变了
Pivot := Root.Left
B := Pivot.Right
Pivot.Right = Root
Root.Left = B
// 只有Root和Pivot变化了高度
Root.UpdateHeight()
Pivot.UpdateHeight()
return Pivot
}
// 单左旋操作,看图说话
func LeftRotation(Root *AVLTreeNode) *AVLTreeNode {
// 只有Pivot和B,Root位置变了
Pivot := Root.Right
B := Pivot.Left
Pivot.Left = Root
Root.Right = B
// 只有Root和Pivot变化了高度
Root.UpdateHeight()
Pivot.UpdateHeight()
return Pivot
}
// 先左后右旋操作,看图说话
func LeftRightRotation(node *AVLTreeNode) *AVLTreeNode {
node.Left = LeftRotation(node.Left)
return RightRotation(node)
}
// 先右后左旋操作,看图说话
func RightLeftRotation(node *AVLTreeNode) *AVLTreeNode {
node.Right = RightRotation(node.Right)
return LeftRotation(node)
}
// 添加元素
func (tree *AVLTree) Add(value int64) {
// 往树根添加元素,会返回新的树根
tree.Root = tree.Root.Add(value)
}
func (node *AVLTreeNode) Add(value int64) *AVLTreeNode {
// 添加值到根节点node,如果node为空,那么让值成为新的根节点,树的高度为1
if node == nil {
return &AVLTreeNode{Value: value, Height: 1}
}
// 如果值重复,什么都不用做,直接更新次数
if node.Value == value {
node.Times = node.Times + 1
return node
}
// 辅助变量
var newTreeNode *AVLTreeNode
if value > node.Value {
// 插入的值大于节点值,要从右子树继续插入
node.Right = node.Right.Add(value)
// 平衡因子,插入右子树后,要确保树根左子树的高度不能比右子树低一层。
factor := node.BalanceFactor()
// 右子树的高度变高了,导致左子树-右子树的高度从-1变成了-2。
if factor == -2 {
if value > node.Right.Value {
// 表示在右子树上插上右儿子导致失衡,需要单左旋:
newTreeNode = LeftRotation(node)
} else {
//表示在右子树上插上左儿子导致失衡,先右后左旋:
newTreeNode = RightLeftRotation(node)
}
}
} else {
// 插入的值小于节点值,要从左子树继续插入
node.Left = node.Left.Add(value)
// 平衡因子,插入左子树后,要确保树根左子树的高度不能比右子树高一层。
factor := node.BalanceFactor()
// 左子树的高度变高了,导致左子树-右子树的高度从1变成了2。
if factor == 2 {
if value < node.Left.Value {
// 表示在左子树上插上左儿子导致失衡,需要单右旋:
newTreeNode = RightRotation(node)
} else {
//表示在左子树上插上右儿子导致失衡,先左后右旋:
newTreeNode = LeftRightRotation(node)
}
}
}
if newTreeNode == nil {
// 表示什么旋转都没有,根节点没变,直接刷新树高度
node.UpdateHeight()
return node
} else {
// 旋转了,树根节点变了,需要刷新新的树根高度
newTreeNode.UpdateHeight()
return newTreeNode
}
}
// 找出最小值的节点
func (tree *AVLTree) FindMinValue() *AVLTreeNode {
if tree.Root == nil {
// 如果是空树,返回空
return nil
}
return tree.Root.FindMinValue()
}
func (node *AVLTreeNode) FindMinValue() *AVLTreeNode {
// 左子树为空,表面已经是最左的节点了,该值就是最小值
if node.Left == nil {
return node
}
// 一直左子树递归
return node.Left.FindMinValue()
}
// 找出最大值的节点
func (tree *AVLTree) FindMaxValue() *AVLTreeNode {
if tree.Root == nil {
// 如果是空树,返回空
return nil
}
return tree.Root.FindMaxValue()
}
func (node *AVLTreeNode) FindMaxValue() *AVLTreeNode {
// 右子树为空,表面已经是最右的节点了,该值就是最大值
if node.Right == nil {
return node
}
// 一直右子树递归
return node.Right.FindMaxValue()
}
// 查找指定节点
func (tree *AVLTree) Find(value int64) *AVLTreeNode {
if tree.Root == nil {
// 如果是空树,返回空
return nil
}
return tree.Root.Find(value)
}
func (node *AVLTreeNode) Find(value int64) *AVLTreeNode {
if value == node.Value {
// 如果该节点刚刚等于该值,那么返回该节点
return node
} else if value < node.Value {
// 如果查找的值小于节点值,从节点的左子树开始找
if node.Left == nil {
// 左子树为空,表示找不到该值了,返回nil
return nil
}
return node.Left.Find(value)
} else {
// 如果查找的值大于节点值,从节点的右子树开始找
if node.Right == nil {
// 右子树为空,表示找不到该值了,返回nil
return nil
}
return node.Right.Find(value)
}
}
// 删除指定的元素
func (tree *AVLTree) Delete(value int64) {
if tree.Root == nil {
// 如果是空树,直接返回
return
}
tree.Root = tree.Root.Delete(value)
}
func (node *AVLTreeNode) Delete(value int64) *AVLTreeNode {
if node == nil {
// 如果是空树,直接返回
return nil
}
if value < node.Value {
// 从左子树开始删除
node.Left = node.Left.Delete(value)
// 删除后要更新该子树高度
node.Left.UpdateHeight()
} else if value > node.Value {
// 从右子树开始删除
node.Right = node.Right.Delete(value)
// 删除后要更新该子树高度
node.Right.UpdateHeight()
} else {
// 找到该值对应的节点
// 该节点没有左右子树
// 第一种情况,删除的节点没有儿子,直接删除即可。
if node.Left == nil && node.Right == nil {
return nil // 直接返回nil,表示直接该值删除
}
// 该节点有两棵子树,选择更高的哪个来替换
// 第二种情况,删除的节点下有两个子树,选择高度更高的子树下的节点来替换被删除的节点,如果左子树更高,选择左子树中最大的节点,也就是左子树最右边的叶子节点,如果右子树更高,选择右子树中最小的节点,也就是右子树最左边的叶子节点。最后,删除这个叶子节点。
if node.Left != nil && node.Right != nil {
// 左子树更高,拿左子树中最大值的节点替换
if node.Left.Height > node.Right.Height {
maxNode := node.Left
for maxNode.Right != nil {
maxNode = maxNode.Right
}
// 最大值的节点替换被删除节点
node.Value = maxNode.Value
node.Times = maxNode.Times
// 把最大的节点删掉
node.Left = node.Left.Delete(maxNode.Value)
// 删除后要更新该子树高度
node.Left.UpdateHeight()
} else {
// 右子树更高,拿右子树中最小值的节点替换
minNode := node.Right
for minNode.Left != nil {
minNode = minNode.Left
}
// 最小值的节点替换被删除节点
node.Value = minNode.Value
node.Times = minNode.Times
// 把最小的节点删掉
node.Right = node.Right.Delete(minNode.Value)
// 删除后要更新该子树高度
node.Right.UpdateHeight()
}
} else {
// 只有左子树或只有右子树
// 只有一个子树,该子树也只是一个节点,将该节点替换被删除的节点,然后置子树为空
if node.Left != nil {
//第三种情况,删除的节点只有左子树,因为树的特征,可以知道左子树其实就只有一个节点,它本身,否则高度差就等于2了。
node.Value = node.Left.Value
node.Times = node.Left.Times
node.Height = 1
node.Left = nil
} else if node.Right != nil {
//第四种情况,删除的节点只有右子树,因为树的特征,可以知道右子树其实就只有一个节点,它本身,否则高度差就等于2了。
node.Value = node.Right.Value
node.Times = node.Right.Times
node.Height = 1
node.Right = nil
}
}
// 找到值后,进行替换删除后,直接返回该节点
return node
}
// 左右子树递归删除节点后需要平衡
var newNode *AVLTreeNode
// 相当删除了右子树的节点,左边比右边高了,不平衡
if node.BalanceFactor() == 2 {
if node.Left.BalanceFactor() >= 0 {
newNode = RightRotation(node)
} else {
newNode = LeftRightRotation(node)
}
// 相当删除了左子树的节点,右边比左边高了,不平衡
} else if node.BalanceFactor() == -2 {
if node.Right.BalanceFactor() <= 0 {
newNode = LeftRotation(node)
} else {
newNode = RightLeftRotation(node)
}
}
if newNode == nil {
node.UpdateHeight()
return node
} else {
newNode.UpdateHeight()
return newNode
}
}
// 中序遍历
func (tree *AVLTree) MidOrder() {
tree.Root.MidOrder()
}
func (node *AVLTreeNode) MidOrder() {
if node == nil {
return
}
// 先打印左子树
node.Left.MidOrder()
// 按照次数打印根节点
for i := 0; i <= int(node.Times); i++ {
fmt.Println("value:", node.Value, " tree height:", node.BalanceFactor())
}
// 打印右子树
node.Right.MidOrder()
}
// 验证是不是棵AVL树
func (tree *AVLTree) IsAVLTree() bool {
if tree == nil || tree.Root == nil {
return true
}
// 判断节点是否符合 AVL 树的定义
if tree.Root.IsRight() {
return true
}
return false
}
// 判断节点是否符合 AVL 树的定义
func (node *AVLTreeNode) IsRight() bool {
if node == nil {
return true
}
// 左右子树都为空,那么是叶子节点
if node.Left == nil && node.Right == nil {
// 叶子节点高度应该为1
if node.Height == 1 {
return true
} else {
fmt.Println("leaf node height is ", node.Height)
return false
}
} else if node.Left != nil && node.Right != nil {
// 左右子树都是满的
// 左儿子必须比父亲小,右儿子必须比父亲大
if node.Left.Value < node.Value && node.Right.Value > node.Value {
} else {
// 不符合 AVL 树定义
fmt.Printf("father is %v lchild is %v, rchild is %v\n", node.Value, node.Left.Value, node.Right.Value)
return false
}
bal := node.Left.Height - node.Right.Height
if bal < 0 {
bal = -bal
}
// 子树高度差不能大于1
if bal > 1 {
fmt.Println("sub tree height bal is ", bal)
return false
}
// 如果左子树比右子树高,那么父亲的高度等于左子树+1
if node.Left.Height > node.Right.Height {
if node.Height == node.Left.Height+1 {
} else {
fmt.Printf("%#v height:%v,left sub tree height: %v,right sub tree height:%v\n", node, node.Height, node.Left.Height, node.Right.Height)
return false
}
} else {
// 如果右子树比左子树高,那么父亲的高度等于右子树+1
if node.Height == node.Right.Height+1 {
} else {
fmt.Printf("%#v height:%v,left sub tree height: %v,right sub tree height:%v\n", node, node.Height, node.Left.Height, node.Right.Height)
return false
}
}
// 递归判断子树
if !node.Left.IsRight() {
return false
}
// 递归判断子树
if !node.Right.IsRight() {
return false
}
} else {
// 只存在一棵子树
if node.Right != nil {
// 子树高度只能是1
if node.Right.Height == 1 && node.Right.Left == nil && node.Right.Right == nil {
if node.Right.Value > node.Value {
// 右节点必须比父亲大
} else {
fmt.Printf("%v,(%#v,%#v) child", node.Value, node.Right, node.Left)
return false
}
} else {
fmt.Printf("%v,(%#v,%#v) child", node.Value, node.Right, node.Left)
return false
}
} else {
if node.Left.Height == 1 && node.Left.Left == nil && node.Left.Right == nil {
if node.Left.Value < node.Value {
// 左节点必须比父亲小
} else {
fmt.Printf("%v,(%#v,%#v) child", node.Value, node.Right, node.Left)
return false
}
} else {
fmt.Printf("%v,(%#v,%#v) child", node.Value, node.Right, node.Left)
return false
}
}
}
return true
}
func main() {
values := []int64{2, 3, 7, 10, 10, 10, 10, 23, 9, 102, 109, 111, 112, 113}
// 初始化二叉查找树并添加元素
tree := NewAVLTree()
for _, v := range values {
tree.Add(v)
}
// 找到最大值或最小值的节点
fmt.Println("find min value:", tree.FindMinValue())
fmt.Println("find max value:", tree.FindMaxValue())
// 查找不存在的99
node := tree.Find(99)
if node != nil {
fmt.Println("find it 99!")
} else {
fmt.Println("not find it 99!")
}
// 查找存在的9
node = tree.Find(9)
if node != nil {
fmt.Println("find it 9!")
} else {
fmt.Println("not find it 9!")
}
// 删除存在的9后,再查找9
tree.Delete(9)
tree.Delete(10)
tree.Delete(2)
tree.Delete(3)
tree.Add(4)
tree.Add(3)
tree.Add(10)
tree.Delete(111)
node = tree.Find(9)
if node != nil {
fmt.Println("find it 9!")
} else {
fmt.Println("not find it 9!")
}
// 中序遍历,实现排序
tree.MidOrder()
if tree.IsAVLTree() {
fmt.Println("is a avl tree")
} else {
fmt.Println("is not avl tree")
}
}
运行结果:
find min value: &{2 0 1 <nil> <nil>}
find max value: &{113 0 1 <nil> <nil>}
not find it 99!
find it 9!
not find it 9!
value: 3 tree height: 0
value: 4 tree height: 1
value: 7 tree height: 0
value: 10 tree height: 0
value: 23 tree height: 1
value: 102 tree height: 1
value: 109 tree height: 0
value: 112 tree height: 0
value: 113 tree height: 0
is a avl tree
可以看到,它确实是一棵 AVL 树。
PS:我们的程序是递归程序,如果改写为非递归形式,效率和性能会更好,在此就不实现了,理解AVL树添加和删除的总体思路即可。
八、应用场景
AVL 树作为严格平衡的二叉查找树,在 windows 对进程地址空间的管理被使用到。
下一节:某些教程不区分普通红黑树和左倾红黑树的区别,直接将左倾红黑树拿来教学,并且称其为红黑树,因为左倾红黑树与普通的红黑树相比,实现起来较为简单,容易教学。在这里,我们区分开左倾红黑树和普通红黑树。