归并排序是一种分治策略的排序算法。它是一种比较特殊的排序算法,通过递归地先使每个子序列有序,再将两个有序的序列进行合并成一个有序的序列。
归并排序首先由著名的现代计算机之父 John_von_Neumann 在 1945 年发明,被用在了 EDVAC(一台美国早期电子计算机),足足用墨水写了 23 页的排序程序。注:冯·诺依曼(John von Neumann,1903年12月28日-1957年2月8日),美籍匈牙利数学家、计算机科学家、物理学家,是20世纪最重要的数学家之一。
一、算法介绍
我们先介绍两个有序的数组合并成一个有序数组的操作。
- 先申请一个辅助数组,长度等于两个有序数组长度的和。
- 从两个有序数组的第一位开始,比较两个元素,哪个数组的元素更小,那么该元素添加进辅助数组,然后该数组的元素变更为下一位,继续重复这个操作,直至数组没有元素。
- 返回辅助数组。
举一个例子:
有序数组A:[3 8 9 11 13]
有序数组B:[1 5 8 10 17 19 20 23]
[] 表示比较的范围。
因为 1 < 3,所以 1 加入辅助数组
有序数组A:[3 8 9 11 13]
有序数组B:1 [5 8 10 17 19 20 23]
辅助数组:1
因为 3 < 5,所以 3 加入辅助数组
有序数组A:3 [8 9 11 13]
有序数组B:1 [5 8 10 17 19 20 23]
辅助数组:1 3
因为 5 < 8,所以 5 加入辅助数组
有序数组A:3 [8 9 11 13]
有序数组B:1 5 [8 10 17 19 20 23]
辅助数组:1 3 5
因为 8 == 8,所以 两个数都 加入辅助数组
有序数组A:3 8 [9 11 13]
有序数组B:1 5 8 [10 17 19 20 23]
辅助数组:1 3 5 8 8
因为 9 < 10,所以 9 加入辅助数组
有序数组A:3 8 9 [11 13]
有序数组B:1 5 8 [10 17 19 20 23]
辅助数组:1 3 5 8 8 9
因为 10 < 11,所以 10 加入辅助数组
有序数组A:3 8 9 [11 13]
有序数组B:1 5 8 10 [17 19 20 23]
辅助数组:1 3 5 8 8 9 10
因为 11 < 17,所以 11 加入辅助数组
有序数组A:3 8 9 11 [13]
有序数组B:1 5 8 10 [17 19 20 23]
辅助数组:1 3 5 8 8 9 10 11
因为 13 < 17,所以 13 加入辅助数组
有序数组A:3 8 9 11 13
有序数组B:1 5 8 10 [17 19 20 23]
辅助数组:1 3 5 8 8 9 10 11 13
因为数组A已经没有比较元素,将数组B剩下的元素拼接在辅助数组后面。
结果:1 3 5 8 8 9 10 11 13 17 19 20 23
将两个有序数组进行合并,最多进行 n 次比较就可以生成一个新的有序数组,n 是两个数组长度较大的那个。
- 归并操作最坏的时间复杂度为:
O(n),其中n是较长数组的长度。 - 归并操作最好的时间复杂度为:
O(n),其中n是较短数组的长度。
正是利用这个特点,归并排序先排序较小的数组,再将有序的小数组合并形成更大有序的数组。归并排序有两种递归做法,一种是自顶向下,一种是自底向上。
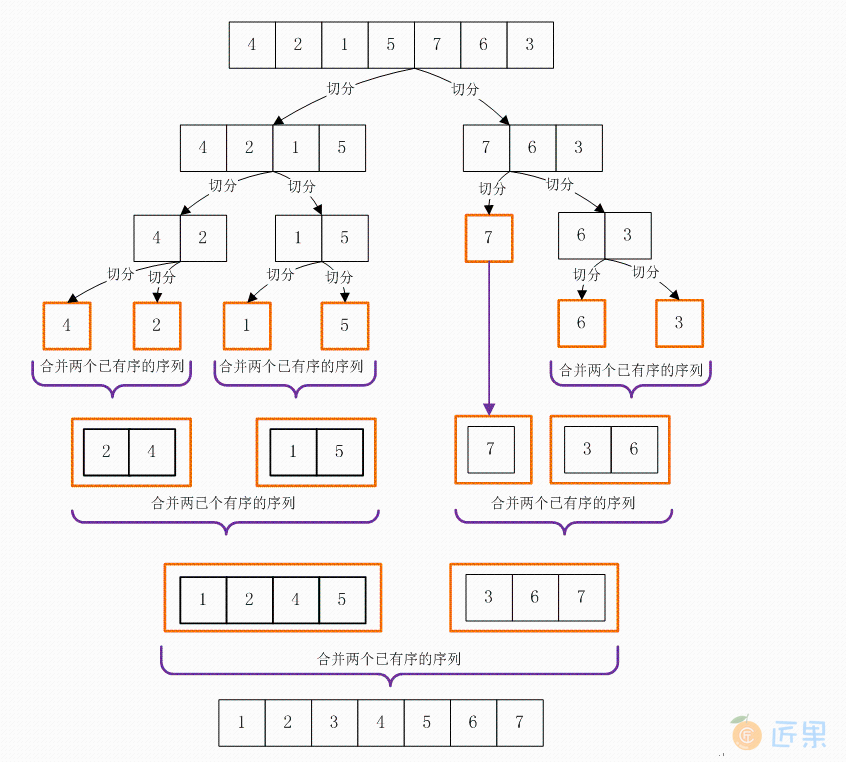
1.1. 自顶向下归并排序
从一个大数组开始,不断地往下切分,如图:
从上往下进行递归,直到切分的小数组无法切分了,然后不断地对这些有序数组进行合并。
每次都是一分为二,特别均匀,所以最差和最坏时间复杂度都一样。归并操作的时间复杂度为:O(n),因此总的时间复杂度为:T(n)=2T(n/2)+O(n),根据主定理公式可以知道时间复杂度为:O(nlogn)。我们可以自己计算一下:
归并排序,每次归并操作比较的次数为两个有序数组的长度: n/2
T(n) = 2*T(n/2) + n/2
T(n/2) = 2*T(n/4) + n/4
T(n/4) = 2*T(n/8) + n/8
T(n/8) = 2*T(n/16) + n/16
...
T(4) = 2*T(2) + 4
T(2) = 2*T(1) + 2
T(1) = 1
进行合并也就是:
T(n) = 2*T(n/2) + n/2
= 2^2*T(n/4)+ n/2 + n/2
= 2^3*T(n/8) + n/2 + n/2 + n/2
= 2^4*T(n/16) + n/2 + n/2 + n/2 + n/2
= ...
= 2^logn*T(1) + logn * n/2
= 2^logn + 1/2*nlogn
= n + 1/2*nlogn
因为当问题规模 n 趋于无穷大时 nlogn 比 n 大,所以 T(n) = O(nlogn)。
因此时间复杂度为:O(nlogn)。
因为不断地递归,程序栈层数会有 logn 层,所以递归栈的空间复杂度为:O(logn),对于排序十亿个整数,也只要:log(100 0000 0000)=29.897,占用的堆栈层数最多 30 层忧。
1.2. 自底向上归并排序
从小数组开始排序,不断地合并形成更大的有序数组。
时间复杂度和自顶向上归并排序一样,也都是 O(nlogn)。因为不需要使用递归,没有程序栈占用,因此递归栈的空间复杂度为:O(1)。
二、算法实现
自顶向下的归并排序递归实现:
package main
import "fmt"
// 自顶向下归并排序,排序范围在 [begin,end) 的数组
func MergeSort(array []int, begin int, end int) {
// 元素数量大于1时才进入递归
if end-begin > 1 {
// 将数组一分为二,分为 array[begin,mid) 和 array[mid,high)
mid := begin + (end-begin+1)/2
// 先将左边排序好
MergeSort(array, begin, mid)
// 再将右边排序好
MergeSort(array, mid, end)
// 两个有序数组进行合并
merge(array, begin, mid, end)
}
}
// 归并操作
func merge(array []int, begin int, mid int, end int) {
// 申请额外的空间来合并两个有序数组,这两个数组是 array[begin,mid),array[mid,end)
leftSize := mid - begin // 左边数组的长度
rightSize := end - mid // 右边数组的长度
newSize := leftSize + rightSize // 辅助数组的长度
result := make([]int, 0, newSize)
l, r := 0, 0
for l < leftSize && r < rightSize {
lValue := array[begin+l] // 左边数组的元素
rValue := array[mid+r] // 右边数组的元素
// 小的元素先放进辅助数组里
if lValue < rValue {
result = append(result, lValue)
l++
} else {
result = append(result, rValue)
r++
}
}
// 将剩下的元素追加到辅助数组后面
result = append(result, array[begin+l:mid]...)
result = append(result, array[mid+r:end]...)
// 将辅助数组的元素复制回原数组,这样该辅助空间就可以被释放掉
for i := 0; i < newSize; i++ {
array[begin+i] = result[i]
}
return
}
func main() {
list := []int{5}
MergeSort(list, 0, len(list))
fmt.Println(list)
list1 := []int{5, 9}
MergeSort(list1, 0, len(list1))
fmt.Println(list1)
list2 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
MergeSort(list2, 0, len(list2))
fmt.Println(list2)
}
输出:
[5]
[5 9]
[1 3 4 5 6 6 6 8 9 14 25 49]
自顶向下递归排序,我们可以看到每次合并都要申请一个辅助数组,然后合并完再赋值回原数组,这样每次合并后辅助数组的内存就可以释放掉,存储空间占用 n,而程序递归栈依旧是 logn 层。自底向上的非递归实现:
package main
import "fmt"
// 自底向上归并排序
func MergeSort2(array []int, begin, end int) {
// 步数为1开始,step长度的数组表示一个有序的数组
step := 1
// 范围大于 step 的数组才可以进入归并
for end-begin > step {
// 从头到尾对数组进行归并操作
// step << 1 = 2 * step 表示偏移到后两个有序数组将它们进行归并
for i := begin; i < end; i += step << 1 {
var lo = i // 第一个有序数组的上界
var mid = lo + step // 第一个有序数组的下界,第二个有序数组的上界
var hi = lo + (step << 1) // 第二个有序数组的下界
// 不存在第二个数组,直接返回
if mid > end {
return
}
// 第二个数组长度不够
if hi > end {
hi = end
}
// 两个有序数组进行合并
merge(array, lo, mid, hi)
}
// 上面的 step 长度的两个数组都归并成一个数组了,现在步长翻倍
step <<= 1
}
}
// 归并操作
func merge(array []int, begin int, mid int, end int) {
// 申请额外的空间来合并两个有序数组,这两个数组是 array[begin,mid),array[mid,end)
leftSize := mid - begin // 左边数组的长度
rightSize := end - mid // 右边数组的长度
newSize := leftSize + rightSize // 辅助数组的长度
result := make([]int, 0, newSize)
l, r := 0, 0
for l < leftSize && r < rightSize {
lValue := array[begin+l] // 左边数组的元素
rValue := array[mid+r] // 右边数组的元素
// 小的元素先放进辅助数组里
if lValue < rValue {
result = append(result, lValue)
l++
} else {
result = append(result, rValue)
r++
}
}
// 将剩下的元素追加到辅助数组后面
result = append(result, array[begin+l:mid]...)
result = append(result, array[mid+r:end]...)
// 将辅助数组的元素复制回原数组,这样该辅助空间就可以被释放掉
for i := 0; i < newSize; i++ {
array[begin+i] = result[i]
}
return
}
func main() {
list := []int{5}
MergeSort2(list, 0, len(list))
fmt.Println(list)
list1 := []int{5, 9}
MergeSort2(list1, 0, len(list1))
fmt.Println(list1)
list2 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
MergeSort2(list2, 0, len(list2))
fmt.Println(list2)
}
输出:
[5]
[5 9]
[1 3 4 5 6 6 6 8 9 14 25 49]
自底向上非递归排序,我们可以看到没有递归那样程序栈的增加,效率比自顶向上的递归版本高
三、算法改进
归并排序归并操作占用了额外的辅助数组,且归并操作是从一个元素的数组开始。我们可以做两点改进:
- 对于小规模数组,使用直接插入排序。
- 原地排序,节约掉辅助数组空间的占用。
我们建议使用自底向上非递归排序,不会有程序栈空间损耗。我们先来介绍一种翻转算法,也叫手摇算法,主要用来对数组两部分进行位置互换,比如数组: [9,8,7,1,2,3],将前三个元素与后面的三个元素交换位置,变成 [1,2,3,9,8,7]。
再比如,将字符串 abcde1234567 的前 5 个字符与后面的字符交换位置,那么手摇后变成:1234567abcde。如何翻转呢?
- 将前部分逆序
- 将后部分逆序
- 对整体逆序
示例如下:
翻转 [1234567abcde] 的前5个字符。
1. 分成两部分:[abcde][1234567]
2. 分别逆序变成:[edcba][7654321]
3. 整体逆序:[1234567abcde]
归并原地排序利用了手摇算法的特征,不需要额外的辅助数组。
首先,两个有序的数组,分别是 arr[begin,mid-1],arr[mid,end],此时初始化 i=begin,j=mid,k=end,从 i~j 为左有序的数组,k~j为右有序的数组,如图:
将 i 向后移动,找到第一个 arr[i]>arr[j]的索引,这个时候,i 前面的部分已经排好序了,begin~i 这些元素已经是两个有序数组的前 n 小个元素。如图:
然后将 j 向后移动,找到第一个 arr[j]>arr[i]的索引,如图:
这个时候,mid~j 中的元素都小于 arr[i],前面已经知道从 begin~i 已经是前 n 小了,所以这两部分 begin~i,mid~j 也是有序的了,我们要想办法将这两部分连接在一起。
我们只需进行翻转,将 i~mid 和 mid,j-1 部分进行位置互换即可,我们可以用手摇算法。具体的代码如下:
package main
import "fmt"
func InsertSort(list []int) {
n := len(list)
// 进行 N-1 轮迭代
for i := 1; i <= n-1; i++ {
deal := list[i] // 待排序的数
j := i - 1 // 待排序的数左边的第一个数的位置
// 如果第一次比较,比左边的已排好序的第一个数小,那么进入处理
if deal < list[j] {
// 一直往左边找,比待排序大的数都往后挪,腾空位给待排序插入
for ; j >= 0 && deal < list[j]; j-- {
list[j+1] = list[j] // 某数后移,给待排序留空位
}
list[j+1] = deal // 结束了,待排序的数插入空位
}
}
}
// 自底向上归并排序优化版本
func MergeSort3(array []int, n int) {
// 按照三个元素为一组进行小数组排序,使用直接插入排序
blockSize := 3
a, b := 0, blockSize
for b <= n {
InsertSort(array[a:b])
a = b
b += blockSize
}
InsertSort(array[a:n])
// 将这些小数组进行归并
for blockSize < n {
a, b = 0, 2*blockSize
for b <= n {
merge(array, a, a+blockSize, b)
a = b
b += 2 * blockSize
}
if m := a + blockSize; m < n {
merge(array, a, m, n)
}
blockSize *= 2
}
}
// 原地归并操作
func merge(array []int, begin, mid, end int) {
// 三个下标,将数组 array[begin,mid] 和 array[mid,end-1]进行原地归并
i, j, k := begin, mid, end-1 // 因为数组下标从0开始,所以 k = end-1
for j-i > 0 && k-j >= 0 {
step := 0
// 从 i 向右移动,找到第一个 array[i]>array[j]的索引
for j-i > 0 && array[i] <= array[j] {
i++
}
// 从 j 向右移动,找到第一个 array[j]>array[i]的索引
for k-j >= 0 && array[j] <= array[i] {
j++
step++
}
// 进行手摇翻转,将 array[i,mid] 和 [mid,j-1] 进行位置互换
// mid 是从 j 开始向右出发的,所以 mid = j-step
rotation(array, i, j-step, j-1)
i = i + step
}
}
// 手摇算法,将 array[l,l+1,l+2,...,mid-2,mid-1,mid,mid+1,mid+2,...,r-2,r-1,r] 从mid开始两边交换位置
// 1.先逆序前部分:array[mid-1,mid-2,...,l+2,l+1,l]
// 2.后逆序后部分:array[r,r-1,r-2,...,mid+2,mid+1,mid]
// 3.上两步完成后:array[mid-1,mid-2,...,l+2,l+1,l,r,r-1,r-2,...,mid+2,mid+1,mid]
// 4.整体逆序: array[mid,mid+1,mid+2,...,r-2,r-1,r,l,l+1,l+2,...,mid-2,mid-1]
func rotation(array []int, l, mid, r int) {
reverse(array, l, mid-1)
reverse(array, mid, r)
reverse(array, l, r)
}
func reverse(array []int, l, r int) {
for l < r {
// 左右互相交换
array[l], array[r] = array[r], array[l]
l++
r--
}
}
func main() {
list := []int{5}
MergeSort3(list, len(list))
fmt.Println(list)
list1 := []int{5, 9}
MergeSort3(list1, len(list1))
fmt.Println(list1)
list2 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
MergeSort3(list2, len(list2))
fmt.Println(list2)
list3 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3, 45, 67, 2, 5, 24, 56, 34, 24, 56, 2, 2, 21, 4, 1, 4, 7, 9}
MergeSort3(list3, len(list3))
fmt.Println(list3)
}
输出:
[5]
[5 9]
[1 3 4 5 6 6 6 8 9 14 25 49]
[1 1 2 2 2 3 4 4 4 5 5 6 6 6 7 8 9 9 14 21 24 24 25 34 45 49 56 56 67]
我们自底开始,将元素按照数量为 blockSize 进行小数组排序,使用直接插入排序,然后我们对这些有序的数组向上进行归并操作。
归并过程中,使用原地归并,用了手摇算法,代码如下:
func rotation(array []int, l, mid, r int) {
reverse(array, l, mid-1)
reverse(array, mid, r)
reverse(array, l, r)
}
因为手摇只多了逆序翻转的操作,时间复杂度是 O(n),虽然时间复杂度稍稍多了一点,但存储空间复杂度降为了 O(1)。
归并排序是唯一一个有稳定性保证的高级排序算法,某些时候,为了寻求大规模数据下排序前后,相同元素位置不变,可以使用归并排序。
下一节:堆排序( Heap Sort )由威尔士-加拿大计算机科学家 J. W. J. Williams 在 1964 年发明,它利用了二叉堆 (A binary heap) 的性质实现了排序,并证明了二叉堆数据结构的可用性。同年,美国籍计算机科学家 R. W. Floyd 在其树排序研究的基础上,发布了一个改进的更好的原地排序的堆排序版本。堆排序属于选择类排序算法。